Page 212 - 《应用声学》2025年第3期

746 2025 年 5 月

于声波速度与正常压实或欠压实泥岩地层的垂直 再次进行回归分析，进一步确定如伊顿常数等相关
有效应力间存在直接关系，因此可结合 Terzaghi 线 系数并进行二次计算。直到二者数据吻合或满足
性方程开展地层压力计算，从而建立基于声波测井 一定误差后，将此时得到的地层压力数据视为评价
数据的地层压力求取方法。 结果。
目前常通过伊顿法利用声波测井数据计算地 具体方法思路如图1所示。
层压力，其计算公式为
ܦฉ฾̌ ࠛए฾̌
∆tn
( ) N
p p = p o − (p o − p b ) , (1)
∆to
۳̆ܦฉ฾̌஝૶ᄊڡ ۳̆ࠛए฾̌஝૶ᄊڡ
3 ࡏԍҧᮕ฾വی ࡏԍҧᮕ฾വی
式 (1) 中，p p 为地层孔隙压力当量密度，g/cm ；p o
3
为上覆岩层压力当量密度，g/cm ；p b 为静液柱压力
ࠄ฾གಣ಩ ࠄ฾གಣ಩
3
当量密度，g/cm ；∆tn 为正常压实声波时差，µs/ft；
∆to为实测声波时差，µs/ft；N 为伊顿指数。 വیТ᪄Ԡ஝ᆸࠀ വیТ᪄Ԡ஝ᆸࠀ
从公式 (1) 可见，伊顿指数是准确求取地层压
力的关键参数。而在不同区块以及不同地层，都对 ក͉ፇ౧Ѻኙ ក͉ፇ౧Ѻኙ
应不同的伊顿指数。若依据经验值确定伊顿指数，
将影响地层压力的精准求取。 උࠫឨࣀᣗܸ
ក͉ፇ౧උࠫ
此外，由于泥页岩在低渗透油藏中占据重要地
位，前人根据泥页岩密度与孔隙度之间的相互关系 උࠫឨࣀՌေ
及其随埋深的变化关系，建立了利用密度测井数据
ក͉ፇ౧ᆸࠀ
求取地层压力的方法。其求取模型为
( ) a
D en 图 1 方法思路图
ρ p = ρ o − (ρ o − ρ w ) , (2)
D n
en Fig. 1 Method diagram
3
式(2)中，ρ p 为地层压力当量密度计算值，g/cm ；ρ o
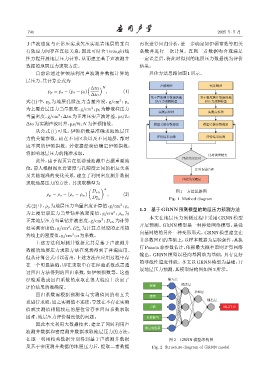
1.2 基于GRNN预测模型的地层压力预测方法
3
为上覆岩层压力当量钻井液密度值，g/cm ；ρ w 为
本文在地层压力预测过程中采用 GRNN 模型
正常地层压力当量钻井液密度，g/cm ；D en 为计算
3
开展预测。GRNN 模型是一种神经网络模型，是径
3
n
处实测密度值，g/cm ；D en 为计算点对应的正常趋
势线上的密度值，g/cm ；a为系数。 向基网络的另外一种变形形式。GRNN模型建立在
3
非参数回归的基础上，以样本数据为后验条件，其执
上述方法利用测井数据尤其是基于声波测井
行Parzen非参数估计，依据最大概率原则计算网络
数据的地层压力求取方法在现场得到了普遍应用。
输出。GRNN 模型以径向基网络为基础，具有良好
但从计算公式可以看出，上述方法在应用过程中存
的非线性逼近性能。本文以 GRNN 模型为基础，开
在一个明显缺陷，即在求取中存在经验系数或需通
展地层压力预测，其模型结构图如图2所示。
过回归方法得到的回归系数，如伊顿指数等。这些
经验系数或回归系数的求取在很大程度上决定了 ᣥКࡏ
评价结果的准确度。 ງए ᬥեࡏ
ර֗ࡏ
回归系数需根据预测值与实测值间的相互关 ࠛए
系进行求取，加之实测值不连续，导致在不存在实测 ᣥѣࡏ
ܦฉ ڡࡏԍҧ
值或实测值相隔较远的层位常存在回归系数求取
困难、地层压力评价精度低的问题。 ᒭཀྵͬᯱ
因此本文利用大数据技术，建立了同时利用声
ڡࡏႃ᫾ဋ
波测井数据和密度测井数据求取地层压力的方法。
在逐一利用相关数据分别得到基于声波测井数据 图 2 GRNN 模型结构图
及基于密度测井数据的地层压力后，提取二者数据 Fig. 2 Structure diagram of GRNN model