Page 240 - 《应用声学》2025年第3期

774 2025 年 5 月


ᎥᬞᣉՔ᫂ए(૱ካੇฉ᫂)
y 1 = A 1 sin(2πf · t),

(1) 0.06 λ/4 λ/2 3λ/4 λ 5λ/4
y 2 = A 2 sin(2πf · t + φ).

0.05
后反射面回波的激发时间更晚、传播路径更远，
两者共同作用引起相位变化 ∆φ = 4π(d/λ)。且前 0.04
后反射面截面面积变化趋势相反 (从大到小、从小 Ԧ࠱ጇ஝ 0.03
到大)，回波间存在固有的相位差 π，故y 1 与 y 2 之间
的总相位差φ = ∆φ − π = 4π(d/λ) − π。叠加后的 0.02
缺陷回波幅值随缺陷尺寸d周期性变化，为 0.01

y = y 1 + y 2 0
0 20 40 60 80 100 120 140 160 180
= A 1 sin(2πf · t) + A 2 sin[2πf · t + φ(d)]. (2) ᮠဋ/kHz
(a) Ԧ࠱ጇ஝జጳ
由于反射面回波能量长度有限，信号干涉现象
1.0
仅在缺陷尺寸相对较小时，于两组回波中间交叠处
32 kHz
显现。随着缺陷尺寸或检测频率增大，前反射面回 λ/4
0.5
波与后反射面回波将逐渐分离，最终形成两个独立
的波包。 0 64 kHz ԥ࢏ λ/2

1.1 有限元分析 ॆʷӑࣨϙ 96 kHz ӭ࢏ 3λ/4
建立外径100 mm、壁厚2 mm的有限元钢管仿 -0.5 128 kHz ԥ࢏ λ
真模型，基于前期研究，在检测位置处环状点集合 ӭ࢏
160 kHz 5λ/4
施加周向集中力，可激发检测所用的 T(0,1) 扭转模 -1.0
0 0.04 0.08 0.12 0.16 0.2
态导波 [25] 。于模型中段设置轴向长度为 25.4 mm ௑ᫎ/ms
的圆柱形模拟缺陷，由于缺陷深度不影响反射系数 (b) Чیڀฉॎ࿄
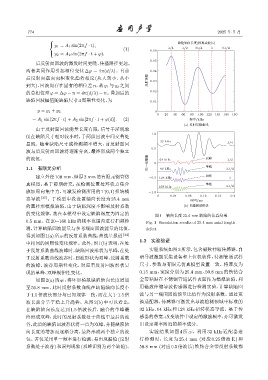
的变化规律，故在本模型中设定缺陷深度为固定的 图 1 轴向长度 25.4 mm 缺陷的仿真结果
0.5 mm。在 20∼160 kHz 的频率范围内进行扫频检 Fig. 1 Simulation results of 25.4 mm axial length
测，计算缺陷回波能量与参考端面回波能量的比值， defect

得到如图1(a)所示的反射系数曲线，曲线呈报道 [24]
1.2 实验验证
中相同的周期性变化规律。此外，图1(b)表明，在处
于反射系数曲线波峰时，缺陷回波形状为单峰，在处 实验系统如图3 所示，包含磁致伸缩传感器、自
于反射系数曲线波谷时，回波形状为双峰，反射系数 研导波激励采集设备和上位机软件，待测管道试样
的波峰、波谷周期性变化，对应着反射回波形状呈 尺寸、参数与有限元仿真模型设置一致。将厚度为
现的单峰、双峰规律性变化。 0.15 mm，宽度分别为 25.4 mm、50.8 mm 的铁钴合
如图 2(a) 所示，将环形模拟缺陷轴向长度增加 金带粘贴在不锈钢管道试件表面作为模拟缺陷，利
至 50.8 mm，此时反射系数曲线在缺陷轴向长度小 用磁致伸缩导波传感器进行检测实验，计算缺陷回
于1.5 倍波长部分与已知规律一致，而在大于 1.5 倍 波与另一端面回波能量比值作为反射系数。通过更
波长部分呈平稳上升趋势。从图 2(b) 中可以看出， 换适配器，传感器可激发出导波检测领域中标准的
在缺陷轴向长度达到 1.5 倍波长后，融合的单峰最 32 kHz、64 kHz 和 128 kHz 扭转模态导波。基于传
终形成双峰，此时的反射系数处于曲线中最后的波 感器的带宽，改变软件中设定的激励频率，亦可激发
谷，此后的缺陷回波形状将一直为双峰，并随缺陷轴 出设定频率附近的频率成分。
向长度的增加而逐渐分离，最终形成两个独立的波 实验结果如图 4 所示，利用 32 kHz 适配器进
包。若仅采用单一频率进行检测，易出现漏检(反射 行检测时，长度为 25.4 mm (对应 0.25 倍波长) 和
系数处于波谷)和误判现象(双峰识别为两个缺陷)。 50.8 mm (对应 0.5 倍波长) 铁钴合金带反射系数都