Page 48 - 201806

878 2018 年 11 月

由图 5 可以看到，二者基本是一个线性的关系， 依次为500、1500、3000、5000、10000、20000。每次加
由非线性声波方程的一阶摄动解 [20] 可知 载结束后进行检测，并分别取不同激励电压下的结
1 2 2 果进行对比，观察检测信号中谐波激发效率 (分别
A 2 = A k βx. (24)
0
8
由于在实验时，传播距离 x 一定，波数 k 一定， 以增益补偿后二次谐波、三次谐波幅度与基波幅度
的比值表示)随试样疲劳程度的变化关系。
同种材料其非线性系数 β 不变，因此二者应是一个
近似的线性关系，如图 5 中红色虚线所示，与实验标
定结果基本吻合，由此可以判定该实验系统可以进
行非线性声学检测的相关实验研究。由图 5 中的红
色虚线看到，其与 y 轴的截距为实验系统的初始非
线性，可能与实验中耦合剂、探头以及仪器本身所
带入的非线性有关，在进行相关实验时可以剔除，但
其值与材料本身引起的非线性相比来说很小，并不
影响实验中相关问题的分析。基于以上分析，进行
以下实验研究。

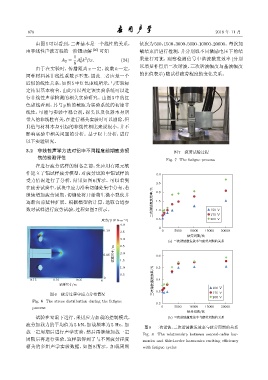
3.2 非线性声学方法对铝中不同程度前期疲劳损 图 7 疲劳试验过程
伤的检测评估 Fig. 7 The fatigue process
在进行疲劳试样的制备之前，先应用有限元软
件建立了铝试样疲劳模型，对疲劳试验中铝试样的 3.0
受力情况进行了分析，结果如图 6 所示。可以看到
2.5
在疲劳试验中，试块中应力沿着切缝处集中分布，若
继续增加疲劳周期，切缝处将开始萌生微小裂纹并 2.0
逐渐向前延伸扩展。根据模型的计算，选取合适参 ̄൓ៈฉ༏ԧ஍ဋ/% 1.5
数对试样进行疲劳试验，过程如图7所示。 1.0 150 V
175 V
6
ऄҧ/(10 NSm -2 ) 0.5 200 V
4.0
0
0.10 0 5000 10000 15000 20000
3.5
Ⴕҷևర/൓
3.0
(a) ̄൓ៈฉ༏ԧ஍ဋˁႵҷևరᄊТጇ
2.5
តನࡇࠪ/m 2.0
0.05 1.5 0.6

1.0 0.5
0.5
0
0.15 0.10 0.05 0 ʼ൓ៈฉ༏ԧ஍ဋ/% 0.4
តನࡇࠪ/m 150 V
图 6 疲劳过程中应力分布情况 0.3 175 V
200 V
Fig. 6 The stress distribution during the fatigue
0.2
process 0 5000 10000 15000 20000
Ⴕҷևర/൓
试验在室温下进行，采用应力加载的控制模式， (b) ʼ൓ៈฉ༏ԧ஍ဋˁႵҷևరᄊТጇ
疲劳加载力的平均值为 5 kN，加载频率为 5 Hz。加
图 8 二次谐波、三次谐波激发效率与疲劳周期的关系
载一定周期后进行声学实验，然后再继续加载一定
Fig. 8 The relationship between second-order har-
周期后再进行实验，这样就得到了与不同疲劳程度 monics and third-order harmonics exciting efficiency
相关的多组声学实验数据，如图 8 所示。加载周期 with fatigue cycles