Page 46 - 201806

876 2018 年 11 月

˙
项，并且随着位错密度Λ的增加，其非线性项的系数 σ (+0, t) = κf (−ct) − P, (12)
变大，由此而引起的声波非线性现象也更明显。我 ˙ u (+0, t) = − ch (−ct) . (13)
˙
们通过实验对其进行了验证，实验结果在3.2节中。
定义裂纹结合面u (0, t)为
I
1
u (0, t) = [u (−0, t) + u (+0, t)] , (14)
b
2
由此可得到裂纹结合面动态力为
τ M L L N
∂u (0, t)
G (y) = −κ
r ∂x
θ
κ [ ]
˙
˙
= − f (−ct) + ˙g (ct) + h (−ct) , (15)
O
2
图 1 位错弦模型 裂纹间距的变化为
Fig. 1 The dislocation monopole model
y (t) = u (+0, t) − u (−0, t) , (16)
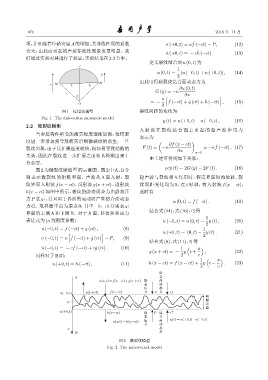
2.2 微裂纹模型
入 射 波 在 裂 纹 结 合 面 上 引 起 的 超 声 波 作 用 力
当金属构件所受的疲劳程度逐渐加强，位错密
表示为
度进一步增加将导致疲劳后期微裂纹的萌生，一旦 ( )
∂f (x − ct) ˙
裂纹出现，由于其扩展速度较快，很容易导致结构的 F (t) = −κ ∂x = −κf (−ct) . (17)
失效，因此在裂纹进一步扩展之前将其检测出来十 x=0
由上述可得到如下关系：
分必要。
图2为微裂纹模型 [6] 的示意图。图2中A、B分 ρc ˙y (t) = 2G (y) − 2F (t) . (18)
别表示微裂纹的粗糙界面，声波从 A 面入射，裂 超声波与裂纹相互作用时，假定界面初始位移、裂
纹界面入射波 f(x − ct)、反射波 g(x + ct)、透射波 纹间距变化均为 0，在 t 时刻，有入射波 f(x − ct)，
h(x − ct) 如图中所示，裂纹的静态闭合力由静态压 此时有
力 P 表示，并且由于界面的运动而产生结合面动态
u (0, t) = f (−ct) . (19)
力 G。取界面中点为原点 0，其中 −0，+0 分别表示
结合式(14)、式(16)，可得
界面的上侧 A 和下侧 B。对于 A 面，其位移和应力
1
表达式为(κ为刚度系数) u (−0, t) = u (0, t) − y (t) , (20)
2
u (−0, t) = f (−ct) + g (ct) , (8) 1
u (+0, t) = (0, t) − y (t) . (21)
[ ] 2
˙
σ (−0, t) = κ f (−ct) + ˙g (ct) − P, (9)
结合式(8)、式(11)，可得
˙
˙ u (−0, t) = − cf (−ct) + c˙g (ct) . (10) 1 ( x )
g (x + ct) = − y t + , (22)
同样对于B面： 2 c
1 ( x )
u (+0, t) = h (−ct) , (11) h (x − ct) = f (x − ct) + y t − . (23)
2 c
ፇ
A Ռ
u↼x֒t↽/f↼x֓ct↽⇁g↼x⇁ct↽ ᭢ ᭧
গ ү
ԍ গ
u↼֓֒t↽ g↼x⇁ct↽ f↼x֓ct↽ ҧ P ҧ G
ዤ
ጀ

ႍ
᭧
u↼⇁֒t↽
h↼x֓ct↽ ᭢ P ፇ G
গ Ռ
u↼x֒t↽/h↼x֓ct↽ ԍ ᭧ y↼t↽/u↼⇁֒t↽֓u↼֓֒t↽
ҧ ү
x গ
B ҧ
图 2 微裂纹模型
Fig. 2 The micro-crack model