Page 41 - 201806

第 37 卷 第 6 期 刘泽等： 充水黏弹性管道的频散曲线计算分析 871

(3)由图3 发现，在频散曲线中出现了α 模态，α 行比较 [8] ，证明谱方法计算黏弹性管道频散曲线不
模态不存在截止频率，仅在充液状态下存在，和0阶 仅误差小、速度快，且高阶模态随着频率增加到一
对称波趋势相似，相速度在 0∼20 kHz 附近减小至 定程度时会出现截止频率。
1000 m/s，20 kHz 以后逐渐上升并稳定在水横波速
度附近。α 模态在低频时以径向位移为主，高频时 2.0
在管壁上主要是弯曲运动，类似于Stoneley波 [10] 。 VT6
3.2 黏弹性管道 1.5 VT4 VT5 VT7
VT3
黏弹性材料的参数一般是根据实验测得的复
杨氏模量E 和复泊松比ν 推导出的： c p /(kmSs -1 ) 1.0 VT2

′
′
E = E (1 − iη E ) , ν = ν (1 − iη ν ) , (16) VT1
0.5 VT0
8
氯丁橡胶 E = 4 × 10 Pa, ν = 0.49，损耗因子
′
′
η E = 0.2, η ν = 0，计算数据如表3所示。
0
根据 LLΘ = k MΘ，利用 MATLAB 数值编 0 10 20 30 40 50 60 70 80 90 100
2
d
z
f⊳kHz
程，得出频散和衰减结果如图 4 和图 5 所示，其中，
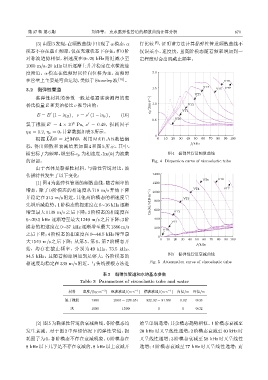
横坐标f 为频率，纵坐标c p 为相速度，Im(k)为波数 图 4 黏弹性管道频散曲线
的虚部。 Fig. 4 Dispersion curve of viscoelastic tube
由于壳体是黏弹性材料，与弹性管道对比，波
传播特性发生了以下变化： 1400
VT5 VT6
(1)图4 为黏弹性管道的频散曲线，随着频率的 1200
增加，除了 0 阶模态的相速度从 718 m/s 开始下降 1000 VT4 VT7
并稳定在 313 m/s 附近，其他高阶模态的相速度呈 800 VT3
先增后减趋势。1阶模态的相速度在0∼16 kHz逐渐 Im(k)/(dBSm -1 )
增至最大 1138 m/s 之后下降；2 阶模态的相速度在 600 VT2
0∼29.5 kHz 逐渐增至最大1240 m/s之后下降；3阶 400
VT1
模态的相速度在 0∼37 kHz 逐渐增至最大 1386 m/s 200
VT0
之后下降；4 阶模态的相速度在 0∼44.5 kHz 增至最
0
大 1549 m/s 之后下降；从第 5、第 6、第 7 阶模态开 0 10 20 30 40 50 60 70 80 90 100
f⊳kHz
始，均存在截止频率，分别为 49 kHz、73.5 kHz、
94.5 kHz。且随着频率增加到足够大，各阶模态的 图 5 黏弹性管道衰减曲线
相速度均稳定在 330 m/s 附近。与传统搜根方法进 Fig. 5 Attenuation curve of viscoelastic tube

表 3 黏弹性管道和水的基本参数
Table 3 Parameters of viscoelastic tube and water

材料 密度/(kg·m −3 ) 纵波波速/(m·s −1 ) 横波波速/(m·s −1 ) 内径/m 外径/m
氯丁橡胶 1300 2306 − 228.35i 322.92 − 31.98i 0.02 0.03

水 1000 1500 0 0 0.02

(2) 图5为黏弹性管道的衰减曲线，各阶模态均 始呈单调递增；其余模态趋势相似。1阶模态衰减至
发生衰减。对于图 2 中理想情况下的弹性管道，损 20 kHz 时又呈线性递增；2 阶模态衰减至 40 kHz 时
耗因子为 0，各阶模态不存在衰减现象。0 阶模态在 又呈线性递增；3 阶模态衰减至 58 kHz 时又呈线性
8 kHz以下几乎是不存在衰减的，8 kHz 以上衰减开 递增；4 阶模态衰减至 77 kHz 时又呈线性递增；而