Page 42 - 201806

872 2018 年 11 月

第 5、第6、第7阶模态衰减近似呈线性递减。所有模 1800 m/s∼2510 m/s之间。由图6和图7得出W1和
态随频率的增加，衰减逐渐稳定在 200 dB/m 附近。 W2模态的相速度仍稍有下降，衰减近似为0 dB/m，
从图 4 和图 5 中可以得出，各阶模态相速度最大值 而其他各模态的相速度充水高于未充水，证明这两
所对应的频率比衰减最低点对应的频率偏小。 种模态以径向位移为主在水中传播，能量主要集中
充水后，与空心黏弹性管道对比，波传播特性 在水中，但由于水和黏弹性管道的耦合作用，仍有
发生了以下变化： 部分能量向黏弹性管道泄漏。图4 和图 6 分析表明，
(1)图6 为充水黏弹性管道频散曲线，与空心黏 除 W1 和 W2 模态外，充水与未充水各阶模态变化
弹性管道各阶模态趋势不变。由图 4 和图 6 对比得 是一致的，总体随着频率的增加，衰减程度逐渐下降
出充水黏弹性管道比未充水黏弹性管道在同一频 并稳定在200 dB/m附近。
率下的相速度低，0阶模态的相速度从516 m/s开始
1400
下降并稳定在 287 m/s 附近，其他高阶模态的相速 VT6
度呈先增后减趋势。1 阶模态的相速度在0∼15 kHz 1200 VT5 VT7
逐渐增至最大 1173 m/s 之后下降；2 阶模态的相 1000 VT4
速度在 0∼29 kHz 逐渐增至最大 1381 m/s 之后下 800 VT3
降；3 阶模态的相速度在 0∼38 kHz 逐渐增至最大 Im(k)/(dBSm -1 )
1528 m/s之后下降；4 阶模态的相速度在 0∼45 kHz 600 VT2
增至最大 1663 m/s 之后下降；从第 5、第 6、第 7 阶 400
VT1
模态开始，均存在截止频率，分别为49 kHz、73 kHz、 200 VT0
W1 W2
94.5 kHz。并且随着频率增加到足够大，各阶模态
0
的相速度均稳定在350 m/s附近。 0 10 20 30 40 50 60 70 80 90 100
f⊳kHz
3.0
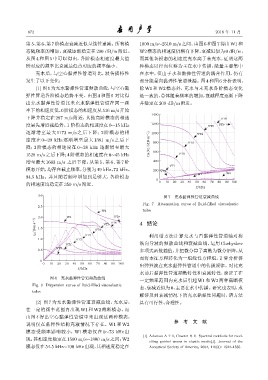
图 7 充水黏弹性管道衰减曲线
Fig. 7 Attenuation curve of fluid-filled viscoelastic
2.5
W2 tube
2.0 W1 VT7
c p /(kmSs -1 ) 1.5 VT4 VT5 VT6 4 结论

1.0 VT2 VT3 利用谱方法计算充水与否黏弹性管道轴对称
纵向导波的频散曲线和衰减曲线，运用 Chebyshev
VT1
VT0
0.5 多项式函数插值，并把微分算子离散为微分矩阵，从
而将本征方程转化为一组线性方程组，计算分析得
0
0 10 20 30 40 50 60 70 80 90 100 出弹性波在充水黏弹性管道中的传播规律。对比充
f⊳kHz
水前后黏弹性管道频散特性和衰减特性，验证了在
图 6 充水黏弹性管道频散曲线
一定频率范围内充水后引起 W1 和 W2 两种截断模
Fig. 6 Dispersion curve of fluid-filled viscoelastic
态，衰减近似为0，主要在水中传播。研究也表明，求
tube
解涉及到衰减情况下的充水黏弹性问题时，谱方法
(2) 图 7 为充水黏弹性管道衰减曲线，充水后， 具有可行性、合理性。
在一定的频率范围内出现 W1 和 W2 截断模态，而
由图 4 得出空心黏弹性管道中未出现这两种模态，
参 考 文 献
说明仅在黏弹性结构充液情况下存在。W1 和 W2
模态受频率影响较小，W1 模态仅在 0∼73 kHz 出
[1] Adamou A T I, Craster R V. Spectral methods for mod-
现，其相速度稳定在 1590 m/s∼1800 m/s 之间；W2
elling guided waves in elastic media[J]. Journal of the
模态仅在54.5 kHz∼100 kHz出现，其相速度稳定在 Acoustical Society of America, 2004, 116(3): 1524–1535.