Page 40 - 201806

870 2018 年 11 月

面条件及边界条件替换到 LL 中相对应的行，同时 附近内急剧减小至1600 m/s，50 kHz以后平缓上升
M 矩阵相对应的主对角线元素设置为 0。结构如 并稳定在1850 m/s。其余高阶波随着频率增加总体
表 1所示。 呈现下降趋势，达到一定频率后都稳定在铜管横波
速度附近。
表 1 矩阵 LL 结构 (充水黏弹性圆柱)
d
(2) 充水以后，铜管壳体的振动模态保持不变，
Table 1 Structure of matrix LL
d
由于水和壳体的耦合作用，在 0 阶波和 1 阶波之间
增加了一系列附加波，这些附加波均存在截止频率，
0 0
L V f
在 3300 m/s 附近出现了 “ 阶梯” 状 [6] ，并随着频率
T T N 1 − T T N 1 +1
的增加，速度逐渐下降稳定在铜管横波速度附近。
SS N 1 − SS N 1 +1
0 L V p 0 6
S3
A2 A4
T T N 1 +N 2
5
A1
SS N 1 +N 2 +1 S2
4
0 0 L V s A0 S1
c p /(kmSs -1 ) 3
SS N 1 +2N 2 S0
3 数值分析 2
1
3.1 弹性铜管
0
图1 为弹性圆柱管道，采用柱坐标系，弹性铜管 0 100 200 300 400 500 600
f⊳kHz
和水的参数如表 2 所示，利用 MATLAB 数值编程，
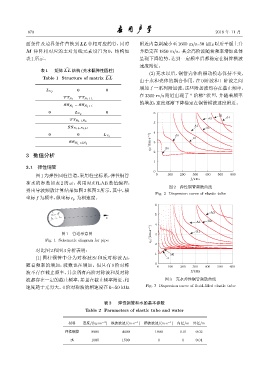
图 2 弹性铜管频散曲线
得出导波频散计算结果如图 2 和图 3 所示，其中，横
Fig. 2 Dispersion curve of elastic tube
坐标f 为频率，纵坐标c p 为相速度。
6
A2
a θ 5
b z
A1 S2
4
c p /(kmSs -1 ) 3
图 1 管道示意图 S1
Fig. 1 Schematic diagram for pipe
2
对比图2和图3分析表明：
1 S0
(1) 圆柱铜管中分为对称波 Si 和反对称波 Ai， α
随着频率的增加，波数也在增加。但只有 0 阶对称 0 0 100 200 300 400 500 600
波不存在截止频率，其余所有高阶对称波和反对称 f⊳kHz
波都存在一定的截止频率，并且在截止频率附近，相 图 3 充水弹性铜管频散曲线
速度趋于无穷大。0阶对称波的相速度在0∼50 kHz Fig. 3 Dispersion curve of fluid-filled elastic tube

表 2 弹性铜管和水的基本参数
Table 2 Parameters of elastic tube and water

材料 密度/(kg·m −3 ) 纵波波速/(m·s −1 ) 横波波速/(m·s −1 ) 内径/m 外径/m
弹性铜管 8900 4400 1940 0.01 0.02

水 1000 1500 0 0 0.01