Page 114 - 201901

110 2019 年 1 月

(2) 求超声波在材料中的衰减系数和相速度
保持探头之间距离不变为 80 mm，在探头之间
放入与不放入实验材料 (橡胶)，将放入材料时的波
形记为 B，未放入实验材料的波形记为 A，其波形
如图 9 所示。对波形 A 和波形 B 的第一个包络点画
线区域内进行频谱分析后，得到幅度谱，其峰值频
率都为 0.77 MHz。根据材料中超声波的衰减系数
a(f) 和相速度 C p (f) 的计算公式，其结果如图 10 所
示。再根据损耗角正切值 tan δ 的计算公式，求出实
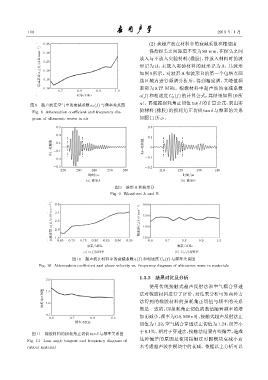
图 8 超声波在空气中的衰减系数 a 1(f) 与频率关系图
验材料 (橡胶) 的损耗角正切值 tan δ 与频率的关系
Fig. 8 Attenuation coefficient and frequency dia-
gram of ultrasonic waves in air 如图11所示。

图 9 波形 A 和波形 B
Fig. 9 Waveform A and B

图 10 超声波在材料中的衰减系数 a(f) 和相速度 C p(f) 与频率关系图
Fig. 10 Attenuation coefficient and phase velocity vs. frequency diagram of ultrasonic wave in materials

1.3.3 结果对比及分析

使用传统接触式超声反射法和空气耦合穿透
法对橡胶材料进行了评价，对结果分析可知两种方
法得到的橡胶材料的损耗角正切值与频率的关系
都是一致的，即损耗角正切值的数值随着频率的增
加而减小，频率为0.8 MHz时，接触式超声反射法正
切值为 1.32；空气耦合穿透法正切值为 1.24，误差小
于6.1%。相对于穿透法，接触法结果有些偏差，造成
图 11 橡胶材料的损耗角正切值 tan δ 与频率关系图
这种偏差的原因是使用接触法时因楔块衰减小而
Fig. 11 Loss angle tangent and frequency diagram of
rubber material 未考虑超声波在楔块中的衰减。依据以上分析可以