Page 116 - 201901

112 0.064 14.7 2019 年 1 月

ᛰѓጇ஝ a 1 ↼f↽/(dBSmm -1 ) 0.062 ᛰѓጇ஝ a↼f↽/(dBSmm -1 ) 14.6

14.5
0.060
14.4
0.058

0.056
0.37 0.38 0.39 0.40 0.41 0.42 0.43 14.3
14.2
ᮠဋ/MHz 0.37 0.38 0.39 0.40 0.41 0.42 0.43
ᮠဋ/MHz
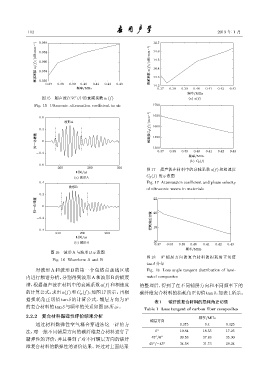
图 15 超声波在空气中的衰减系数 a 1(f) (a) a↼f↽
Fig. 15 Ultrasonic attenuation coefficient in air 1700

0.8 1650
ฉॎA
0.4 ᄱᤴएC p↼f↽/(mSs -1 ) 1600
ॆʷӑࣨϙ 0 1550

1500
0.37 0.38 0.39 0.40 0.41 0.42 0.43
-0.4
ᮠဋ/MHz
(b) C p↼f↽
-0.8
260 280 300 图 17 超声波在材料中的衰减系数 a(f) 和相速度
௑ᫎ/µs
C p(f) 的示意图
(a) ฉॎA
0.4 Fig. 17 Attenuation coefficient and phase velocity
ฉॎB
of ultrasonic waves in materials
0.2 22
ॆʷӑࣨϙ 0

૯Ᏺᝈ൤ѭϙ
-0.2 20

-0.4 18
240 260 280
௑ᫎ/µs
(b) ฉॎB 16
0.37 0.38 0.39 0.40 0.41 0.42 0.43
ᮠဋ/MHz
图 16 波形 A 与波形 B 示意图
图 18 0 铺层方向的复合材料的损耗角正切值
◦
Fig. 16 Waveform A and B
tan δ 分布
对波形 A 和波形 B 的第一个包络点画线区域 Fig. 18 Loss angle tangent distribution of lami-
内进行频谱分析，分别得到波形 A 和波形 B 的幅度 nated composites
谱，根据超声波在材料中的衰减系数 a(f) 和相速度 的整理后，得到了在不同铺层方向和不同频率下的
的计算公式，求出a(f)和C p (f)，如图17所示。再根 碳纤维复合材料的损耗角正切值tan δ，如表1所示。
据损耗角正切值 tan δ 的计算公式，铺层方向为 0 ◦
表 1 碳纤维复合材料的损耗角正切值
的复合材料的tan δ 与频率的关系如图18所示。
Table 1 Loss tangent of carbon fiber composites
2.2.2 复合材料黏弹性评价结果分析 频率/MHz
铺层方向
通过材料黏弹性空气耦合穿透法这一评价方 0.375 0.4 0.425
法，对一批不同铺层方向的碳纤维复合材料进行了 0 ◦ 19.84 18.55 17.25
◦
黏弹性的评价，并且得到了对不同铺层方向的碳纤 45 /0 ◦ 30.53 27.83 25.90
45 /−45 ◦ 34.58 31.73 29.24
◦
维复合材料的黏弹性的评价结果。经过对上面结果