Page 50 - 应用声学2019年第2期

196 2019 年 3 月

1.0 1.0
10 10
0.8 0.8
20 20
0.6 0.6
y/mm 30 0.4 y/mm 30 0.4
40
40
50 50
0.2 0.2
60 60
70 0 70 0
10 20 30 40 50 60 70 10 20 30 40 50 60 70
x/mm x/mm
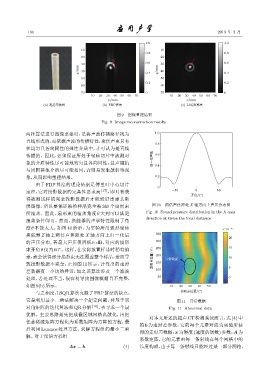
(a) ቸᔇࠄྭڏ (b) FBPካข (c) LSQRካข
图 9 图像重建结果
Fig. 9 Image reconstruction results

两种算法进行图像重建时，是将声波传播路径视为 1.0
直线形式的，而依据声波的传播特性，聚焦声束只有
0.8
在均匀且各向同性的弹性介质中，才可认为是直线
传播的。因此，必须保证所处于聚焦切片中被测对 0.6
象的介质特性尽可能地均匀且各向同性，且声阻抗 ॆʷӑܦԍ 0.4
与周围其他介质尽可能相同，否则易发生散射等现
象，从而影响重建结果。 0.2
由于 FBP 算法的理论依据是傅里叶中心切片
0
定理，它对投影数据的完备性要求高 [17] ，即只有获 -50 0 50
नᝈ/(°)
得被测试样的完全投影数据后才能较好重建其断
层图像，所以要保证被检样品完全被 360 个扇形束 图 10 两倍声焦距处 X 轴方向上声压分布图
所覆盖。因此，扇形束的覆盖角度 θ 大到可以满足 Fig. 10 Sound pressure distribution in the X-axis
direction at twice the focal distance
覆盖条件即可。然而，换能器的声学特性限制了角
度 θ 不能太大，如图 10 所示，为实验所用弧形聚焦 T10 -8
换能器 Z 轴上两倍声焦距处 X 轴方向上归一化后 350
20
的声压分布，若最大声压值降低 6 dB，对应的扇形 300
束开角 θ 仅为 60 。这样，在实际放置样品时稍有偏 250 15
◦
差，就会使得部分扇形束无法覆盖整个样品，进而导 ԧ࠱གͯᎶ/(°) 200 प࣢஝૶ 10
致投影数据不完全，正如图 11 所示，计算出的走时 150
差数据有一小块的异常，加之该算法涉及一个滤波 100 5
处理，若处理不当，很容易导致图像模糊且不完整， 50 0
如图9(b)所示。 10 20 30 40 50
与之相反，LSQR算法克服了FBP算法的缺点， ଌஆགͯᎶ/(°)
它是利用最小二乘法解决一个超定问题，并基于双 图 11 异常数据
对角矩阵的迭代算法和 QR 分解 [18] ，去寻求一个最 Fig. 11 Abnormal data
优解。主要思路是先把成像区域网格离散化，再把
对本文所述的超声CT检测系统而言，式(4) 中
任意稀疏矩阵方程化为系数矩阵为方阵的方程，最
的 b 为走时差参数，它的每个元素对应为实验所获
后利用 Lanczos 处理方法，求解方程组的最小二乘
得的走时差数据；x为慢度(速度的倒数)参数；A为
解。对于反演方程组
系数矩阵，它的元素由每一条射线在每个网格中的

Ax = b. (4) 长度构成，由于每一条射线只能经过某一部分网格，