Page 47 - 应用声学2019年第2期

第 38 卷 第 2 期 蒋剑等： 基于聚焦换能器的超声透射 CT 技术 193

式 (1) 中，J 0 (uξ) 为 第 一 类 零 阶 贝 塞 尔 函 数，u 的宽度 y w 为 1.5 mm，Z 轴方向上的宽度 z w 值为
为 Sommerfeld 积分公式中引用的一个积分变量， 9.7 mm。通过改变聚焦换能器的张角α和曲率半径
其具体形式参见文献 [11] 和文献 [12]，L 为发射 R，探寻以下关系：
面元 S 点到场点 Q 的距离，ζ 是场点 Q 到 G 点的 (1) 当曲率半径 R 为 35 mm 一定时，聚焦换能
距 离 (G 点 为 垂 直 于 平 面 X = X 0 并 经 过 S 点 器张角 α 与换能器声焦距 d f 、聚焦切片 Z 轴方向上
的直线与平面 X = X 0 的交点)， 满足关系式： 的宽度 z w 和 Y 轴方向上的宽度 y w 的关系，如表 1
√
2
2
L = ζ + (X − X 0 ) ，k = 2πf/c 为波数，A 为 所示；
换能器表面 S 点面元到 X 轴的距离，v 为换能器表 (2) 当张角α 为70 一定时，聚焦换能器曲率半
◦
面质点振动速度，而声压p(Q)的表达式为 径 R 与换能器声焦距 d f 、聚焦切片 Z 轴方向上的宽
度z w 和Y 轴方向上的宽度y w 的关系，如表2所示。
p(Q) = jkρcϕ(Q), (2)
从表 1 和表 2 可以看出，该弧形聚焦换能器曲
式(2)中，ρ为介质密度。 率半径一定时，其张角越大，聚焦性能越好，但是在
焦域处波束的平行性越差，使得检测的准确性降低；
S
X
L 1.2
G 1.0
ξ
Q 0.8
A α ॆʷӑܦԍ
R O 0.6
X/X 0 Z
0.4
X/
Y 0.2
w
0
-20 -10 0 10 20
X/mm
(a) X ᣉவՔ
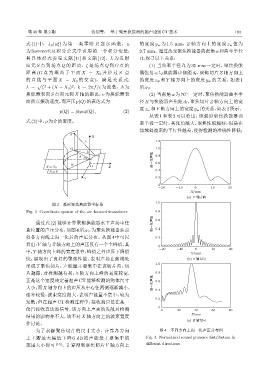
图 3 弧形聚焦换能器坐标系 1.0
Fig. 3 Coordinate system of the arc focused transducer 0.8

通过式 (2) 能够计算聚焦换能器水下声场中任 ॆʷӑܦԍ 0.6
意位置的声压分布，如图4 所示，为聚焦换能器焦点 0.4
处各方向线上归一化后的声压分布。从图 4 中可以 0.2
看出：Y 轴与Z 轴方向上的声压仅有一个主峰值，其 0
-20 -10 0 10 20
中，Y 轴方向上峰的宽度很窄，峰值之外声压下降很 Y/mm
快，展现出了良好的聚焦性能，表明声场在焦域处 (b) Y ᣉவՔ
1.0
形成了聚焦切片，声能量主要集中在该切片内，切
片越薄，对检测越有利；Z 轴方向上峰的宽度较宽， 0.8
正是这个宽度决定着超声 CT能够检测的物体尺寸 ॆʷӑܦԍ 0.6
大小；而X 轴方向上的声压从中心往两侧逐渐减小， 0.4
速率较慢，波束宽度很大，表明声能量不集中，较为
0.2
发散，但在超声 CT检测过程中，接收端只是在某一
位置接收直达波信号，该方向上声束的发散对检测 0 0 20 40 60 80
结果的影响并不大，故不对 X 轴方向上的波束宽度 Z/mm
(c) Z ᣉவՔ
作讨论。
为了求解聚焦切片的尺寸大小，计算各方向 图 4 不同方向上归一化声压分布图
上主瓣最大幅值下降 6 dB 的声能量主要集中的 Fig. 4 Normalized sound pressure distribution in
范围大小即可 [13] 。计算得到聚焦切片 Y 轴方向上 different directions