Page 49 - 应用声学2019年第2期
P. 49
第 38 卷 第 2 期 蒋剑等: 基于聚焦换能器的超声透射 CT 技术 195
实验所用超声波信号的频率为 1 MHz,对应的波长 如图 7 所示,由于采用了聚焦换能器发射和接
为1.5 mm,而声衍射的强弱是同障碍物的大小与声 收信号,其声束聚集性能好,声能量高,声压幅值大,
波波长的比值密切相关的,一般采用 ka = 2πa/λ 相较于声束无法聚焦的平面换能器,能够带来更高
的值来描述,其中,k 为声波的波数,λ 为声波的波 的信噪比,接收信号的波形质量更好。由于接收信
长,a 是代表障碍物相对尺度的量。ka 的值越小 号的信噪比较高,通过拾取直达波信号未到达之前
(ka ≪ 1),声衍射现象越强;ka 的值越大 (ka ≫ 1), 的某一噪声段信号的最大幅值 u max ,并依据实际接
声衍射现象越弱。若取被测样品的尺度 a = 3 mm, 收到的透射波形,再设定一个合适的微小增量 δ,将
可计算出 ka = 12.57 ≫ 1,说明声波衍射效应较弱, (u max + δ) 作为阈值,采用峰值检测法,拾取第一个
那么,接收换能器接收到的声波信号中,无用的干扰 大于该阈值的峰值点,即可轻易地获得发射信号与
信号较少,波形结果更能准确反映被测样品截面的 接收信号的第一个波峰值,对其作差便可很快获取
信息。 走时数据,不仅保证了数据的精确度,而且提高了
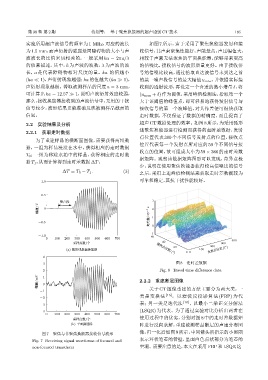
2.2 实验结果及分析 超声CT数据处理的效率。如图 8 所示,为采用弧形
线聚焦换能器进行检测而获得的走时差数据,发射
2.2.1 获取走时数据
点位置代表 360 个不同信号发射点的位置,接收点
为了重建样品的横断面图像,需要获得两组数
位置代表每一个发射点所对应的 59 个不同信号接
据,一组为样品浸没在水中,获得相应的走时数据
收点的位置,故可组成大小为 59 × 360 的走时差数
T 0 ;一组为移除水箱中的样品,获得相应的走时数
据矩阵。观察该数据矩阵图形可以发现,奇异点极
据T 1 ,从而计算得到走时差数据∆T:
少,说明在使用聚焦换能器获得较高信噪比的信号
∆T = T 0 − T 1 . (3) 之后,采用上述峰值检测法来获取走时差数据较为
可靠和稳定,其抗干扰性能较好。
1.0
0.5
٪ܦ 3
ࣨϙ/V 0 2
ᡌࣀ/10 -7 s 1
-0.5 0
-1
-1.0 60
0 100 200 300 400 500 600 700 400
᧔ನག/˔ 40 300
20 200
(a) ऻॎጳᐑཥ૱ᑟ٨ ଌஆགͯᎶ/(°) 100 ԧ࠱གͯᎶ/(°)
0 0
4
3 图 8 走时差数据
2 Fig. 8 Travel time difference data
ࣨϙ/mV 1 0 2.2.2 重建断层图像
-1 关于 CT 图像重建的方法主要分为两大类:一
类是变换法 [15] ,以滤波反投影算法 (FBP) 为代
-2
表;另一类是迭代法 [16] ,以最小二乘正交分解法
-3
-4 (LSQR) 为代表。为了通过实验对比分析出两者在
0 100 200 300 400 500 600 700
᧔ನག/˔ 使用过程中的优劣,分别对图 8 中的走时差数据矩
(b) ࣱ᭧૱ᑟ٨ 阵进行反向求解,重建被测样品断层的声速分布图
图 7 聚焦与非聚焦换能器接收信号波形 像,归一化后如图 9所示,中间箭头所指示的小黑圈
Fig. 7 Receiving signal waveforms of focused and 表示环状笔芯的管壁,里面白色点状部分为笔芯的
non-focused transducer 空洞。需要注意的是,本文在采用FBP和LSQR这