Page 42 - 应用声学2019年第2期

188 2019 年 3 月

3
其纵波波速为 C tl = 5.09 × 10 m/s，横波波速为 局域现象。声波无法用其他非局域态方式通过周期
3 结构，因此能带被分裂，从而产生局域带隙。可以看
C tt = 2.80 × 10 m/s。环氧树脂密度 ρ e = 1.2 ×
3
3
3
10 kg/m ，其纵波波速为C el = 2.83 × 10 m/s，横 到在1407∼5799 Hz 之间出现一个较大的完全带隙，
3
波波速为C et = 1.16 × 10 m/s。 图右侧是对应 ΓX 方向的透射图，在带隙范围内出
磁流变弹性体计算采用磁偶极子模型，Fe 现较大的衰减，在局域频率处衰减最强，出现不对称
颗 粒 密 度 ρ Fe = 7.89 × 10 kg/m ， 橡 胶 密 度 的透射尖峰，这是局域共振 Fano 现象的典型特点。
3
3
3
ρ r = 1.2 × 10 kg/m 。采用磁流变弹性体的拉 这些结果表明：采用磁流变弹性体为包层的二维圆
3
伸性能与剪切性能近似，其泊松比取 0.47 [22] 。剪切 形内核超材料单元，在低频处存在声波局域共振完
模量的改变量与外磁场关系为 [23−24] 全禁带。
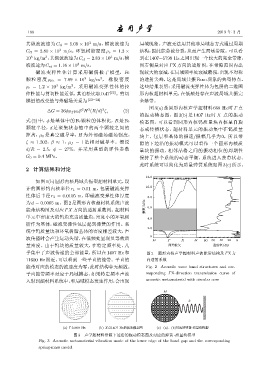
图 3(a) 是圆形内核声学超材料 668 Hz 时 Γ 点
3
2
2
∆G = 36ϕµ f µ 0 β H (R/d) ζ, (2)
的振动模态图，图 3(b) 是 1407 Hz 时 X 点的振动
式 (2) 中，ϕ 是基体中的 Fe 颗粒的体积比，R 是 Fe 模态图，可以看到圆形内核钨质量块内核呈自旋
颗粒半径，d 是聚集状态链中的两个颗粒之间的 态或传播状态，超材料单元的振动集中在钨质量
距离，µ 0 是真空磁导率，H 为外部磁场磁场强度， 块上，包层和基体的振速/振幅几乎为 0，所以带
ζ ≈ 1.202，β ≈ 1，µ f = 1 是相对磁导率。假设 隙的下边沿的振动模式可以看作一个圆形内核质
d/R = 2.5，ϕ = 27%，并采用典型的弹性参数 量块的振动，相邻晶格之间的振动相位的周期性
G 0 = 0.4 MPa。 保持了整个系统的动态平衡，系统进入禁带状态。
此时系统可以简化为质量弹簧系统如图 3(c) 所示，
2 计算结果和讨论

⊲
如图 1(b) 圆形内核局域共振型超材料单元，设
计的圆形钨内核半径 r 1 = 0.01 m，包裹磁流变弹 ⊲
性体后半径 r 2 = 0.0105 m，即磁流变弹性体厚度 ⊲
为 d = 0.0005 m。图 2 是圆形内核超材料系统声波
能带结构图及对应 ΓX 方向的透射系数图。超材料 ᮠဋ/kHz ⊲
单元中密度大的钨块充当质量块，密度小的环氧树 ⊲
脂作为基体，磁流变弹性包层起到弹簧的作用。系
⊲
统中钨质量块和环氧树脂基体的密度相差较大，声
波传播时会产生运动失谐，在低频处呈现负等效质 
M Š X M     
量密度。由于钨块的质量较大，在特定频率处，几 እጞฉᅺ ᤩ࠱ဋ/dB
乎集中了声波传递的全部能量，所以在 1407 Hz 和 图 2 圆形内核声学超材料声波能带结构及 ΓX 方
11600 Hz 附近，可以看到一些平直的能带。平直的 向透射系数
能带对应的模态的波速度为零，此时结构中无频散。 Fig. 2 Acoustic wave band structures and cor-
平直能带频率对应于局域模态，如果特定频率声波 responding ΓX-direction transmission curve of
入射到超材料系统中，和局域模态发生作用，会出现 acoustic metamaterial with circular core

M

k

(a) Γ ག668 Hz (b) Xག1407 Hzᄊ૝үവগڏ (c) (a)nj(b)ࠫऄᄊुዔ-᠏᧚ڱവی
图 3 声学超材料带隙下边沿的振动模态图及对应的弹簧 -质量块模型
Fig. 3 Acoustic metamaterial vibration mode of the lower edge of the band gap and the corresponding
spring-mass model