Page 162 - 201903

444 2019 年 5 月

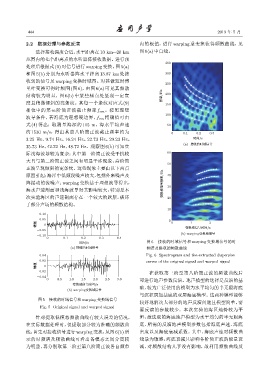
2.2 数据处理与参数反演 内的极值，进行 warping 逆变换获得频散曲线，见
选择接收深度合适、水平距离在10 km∼20 km 图 6(a)中白线。
范围内的七个距离点的水听器阵接收数据。进行预
350
处理后根据式(9)对信号进行warping变换。图 5(a)
和图 5(b) 分别为水听器阵水平距离 13.87 km 处接 300
收到的信号及 warping 变换时域图。对其做短时傅
250
里叶变换可得时频图 (图 6)，由图 6(a) 可见其频散
结构较为明显，图 6(b) 中某些频点处呈现一定宽 ᮠဋ/Hz 200
度且稍微倾斜的亮条纹。其每一个条纹对应式 (9) 150
相位中的第 m 阶简正波截止频率 f cm 。按照理想
100
波导条件，若海底为理想硬边界，f cm 精确值可由
式 (4) 得出：取测量海深约 115 m，海水平均声速 50
约 1530 m/s，得出其前八阶简正波截止频率约为 0 0.1 0.2 0.3
3.25 Hz、9.74 Hz、16.24 Hz、22.73 Hz、29.23 Hz、 ௑ᫎ/s
35.73 Hz、42.22 Hz、48.72 Hz。观察图 6(b) 可知实 (a) ଌஆᄊ௑۫ηՂ
际浅海波导较为复杂：其中第一阶简正波受干扰较 60
大且与第二阶简正波之间有明显干涉现象，高阶简
50
正波呈现倾斜的宽条纹。这些现象主要由以下两点
原因引起：海洋中低频段噪声较大，包括外来噪声及 40
阵摆动的流噪声；warping 变换基于理想波导得出， ԫ૱۫ηՂᮠဋ/Hz
海水声速剖面和浅海波导对其影响较大，特别是本 30
次实验海区的声速剖面存在一个较大的跃层，破坏 20
了部分声场的频散结构。
10
0.10
0.05 0
ࣨϙ 0 0 1 2
-0.05 ԫ૱۫ηՂ௑ᫎ/s
(b) warpingԫ૱۫ηՂ
-0.10
0 0.1 0.2 0.3 0.4
图 6 接收的时域信号和 warping 变换域信号的时
௑ᫎ/s
(a) ଌஆᄊ௑۫ηՂ 频谱及提取的频散曲线
0.04 Fig. 6 Spectrogram and the extracted dispersion
0.02 curves of the original signal and warped signal
ࣨϙ 0
-0.02
在获取第三阶至第八阶简正波的频散曲线后
-0.04
0 0.5 1.0 1.5 2.0 2.5 3.0 可进行地声参数反演。地声模型的选择是反演的基
ԫ૱۫ηՂ௑ᫎ/s
础，较为广泛使用的模型为水平均匀的半无限海底
(b) warpingԫ૱۫ηՂ
与沉积层加基底的双层海底模型。这两种模型能够
图 5 接收的时域信号和 warping 变换域信号
较好地解决大部分的地声反演问题且模型简单，需
Fig. 5 Original signal and warped signal
要反演的参数较少。本次实验的海区地势较为平
针对提取低模态频散曲线有较大误差的情况， 坦，故选取的海底地声模型为水平均匀的半无限海
在实际数据处理时，仅提取部分较为准确的频散曲 底，所需的反演地声模型参数包括海底声速、海底
线：首先对接收信号进行warping变换，从图6(b)所 密度以及海底衰减系数。其中，海底声速对频散曲
示的时频谱及频散曲线可看出各模态之间分离较 线最为敏感，海底衰减只影响各阶简正波的能量衰
为明显，再分别取第三阶至第八阶简正波各自频带 减，对频散结构几乎没有影响，故利用频散曲线反