Page 163 - 201903

第 38 卷 第 3 期 李佳蔚等： 利用气枪声源数据的地声参数反演 445

演海底声速和密度时，衰减系数可以设为任一合理 简正波较难，相比之下，利用传播损失直接拟合更为
值即可，在实际处理中取0.1 dB/波长。本文采用声 简单。实际海洋实验中，海流冲击等会引起接收阵
场计算模型为 Kraken，算法采用自适应模拟退火算 姿势变化，需要根据深度传感器数据、水听器阵接
法 [20] 。如图 6(a) 中，每一阶简正波频散曲线(白线) 收时间及气枪发射声信号时间，对不同距离的阵元
上的白色圆圈代表反演使用的频点数。 进行深度修正，修正结果见图9。
表 1 为七个不同距离数据的反演结果。图 7 给

300
出反演参数及其均值，从图 7中可以看出，不同距离 ࠄᰎଢԩ
஝ϙ͌ᄾ
点反演的海底声速较一致。将反演结果带入求得数 250
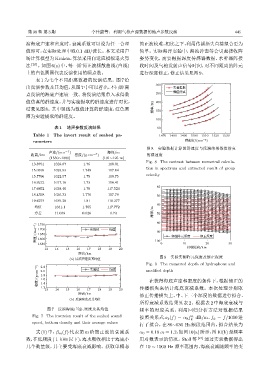
值仿真的群速度，并与实验提取的群速度进行对比， 200
结果见图8。其中黑线为数值计算的群速度，红色圆 ᮠဋ/Hz 150
圈为实验提取的群速度。
100
表 1 地声参数反演结果 50

Table 1 The invert result of seabed pa- 1470 1480 1490 1500 1510 1520 1530
rameters Ꮖᤴए/(mSs -1 )
图 8 实验数据计算的群速度与反演结果数值仿真
声速/(m·s −1 ) 海深/m
距离/km 密度/(g·cm −3 ) 的群速度
(1550∼1880) (101∼125 m)
Fig. 8 The contrast between numerical calcula-
13.8751 1629.87 1.76 118.01
tion in spectrum and extracted result of group
15.0169 1623.93 1.749 117.64
15.7766 1622.57 1.75 118.75 velocity
16.9212 1617.16 1.73 116.41
40
17.6852 1638.40 1.78 117.524
18.4558 1636.33 1.776 117.79 50
19.6274 1649.28 1.81 118.277
60
均值 1631.1 1.765 117.772
๒ງ/m
方差 11.039 0.026 0.73 70
80
1750
ܦᤴ/(mSs -1 ) 1700 ࠄᰎϙ کϙ 90 ࠄᰎ᫼Ћງए ξ൤ງए

1650
1600
1550 100 0 10 20 30
ଌஆᡰሏ/km
13 14 15 16 17 18 19 20
ᡰሏ/km
图 9 实验实测阵元深度及修正深度
(a) Ԧ໦ܦᤴԣХکϙ
Fig. 9 The measured depth of hydrophone and
ࠛए/(gScm -3 ) 2.0 modified depth
2.2
ࠄᰎϙ
کϙ
1.8
1.6
在获得海底声速和密度的条件下，根据修正的
1.4
1.2 传播损失来估计海底衰减系数。本次处理分别取
13 14 15 16 17 18 19 20
ᡰሏ/km
修正传播损失上、中、下三个深度的数据进行拟合。
(b) Ԧ໦ࠛएԣХکϙ
所得衰减系数结果见表 2。根据表 2 中海底衰减与
图 7 反演海底声速、密度及其均值 频率的对应关系，利用回归分析方法对数据结果
Fig. 7 The inversion result of the seabed sound n dB/m、f k = f/1000 进
按照关系式 α b (f) = α 0 f
k
speed, bottom density and their average values
行了拟合，在 80∼630 Hz 频段范围内，拟合结果为
式 (1) 中，β m (f) 代表第 m 阶简正波的衰减系 α 0 = 0.18，n = 1.2，如图10(a)所示，图10(b)是频率
数，在低频段(１kHz以下)，海水吸收相比于海底小 用对数表示的情况。Stoll 等 [21] 通过实验数据得出
几个数量级，其主要受海底衰减影响。获取单模态 在 10 ∼ 1000 Hz 频率范围内，海底衰减随频率的变