Page 168 - 201903

450 2019 年 5 月

特征上的权重衰减快，所映射出空间相当于原始空 训练样本集 D (22×80) 经过 PCA 降维后就转换
间的子空间；C 值过小，可将任意数据映射至线性 成低维数据集 Z (16×80) ，接下来就可以在矩阵 Z 中
可分的空间，但这很可能带来严重的过拟合问题 [8] ， 利用1.3节中的基于核的k-NN进行分类。
因此 C 值的优化尤其重要。k 值的确定采用在一定 1.0
√
范围内 [9] (样本量开平方 m 附近) 进行枚举计算
0.8
确定。
வࣀ᠈࿹ဋ 0.6
2 基 于 核 的k-NN在 水 下 目 标 识 别 中 的 0.4 ግᝠவࣀ᠈࿹
应用 ӭ˔வࣀ᠈࿹
0.2
2.1 数据来源与预处理
0
0 5 10 15 20
将实测的 166 段水下目标噪声信号进行筛选、
˟Ћ˔஝
标记和梅尔频率倒谱系数(Mel frequency cepstrum
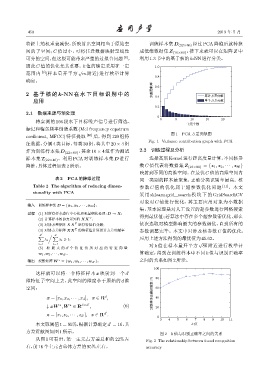
图 1 PCA 方差贡献图
coefficient, MFCC) 特征提取 [10] 后，得到 120 组特
Fig. 1 Variance contribution graph with PCA
征数据，分属 4 类目标，每类 30组，将其中 20 × 4 组
作为训练样本集 D (22×80) ，其余 10 × 4 组作为测试 2.2 训练过程及分析
样本集 T (22×40) 。利用 PCA 对训练样本集 D 进行 选择高斯 Kernel进行距离度量计算，不同核参
降维，具体过程如表2所示。 数 C 值代表将数据集 Z (16×80) = {z 1 , z 2 , · · · , z 80 }
映射到不同的高维空间。在最优C 值的高维空间内
表 2 PCA 的降维过程 同一类别的样本最聚集，正确分类识别率最高。核
Table 2 The algorithm of reducing dimen- 参数 C 值的优化属于超参数优化问题 [11] ，本文
sionality with PCA
采用 sklearn.grid_search 模块下的 GridSearchCV
对象对 C 值进行优化，其主要应用对象为小数据
输入 训练样本集 D = {x 1 , x 2 , · · · , x 80 }。
集，基本原理是对人工设置的超参数进行网格搜索
过程 (1) 对所有样本进行中心化和无量纲化处理：D → X； 得到最优值；若算法中存在多个超参数需优化，那么
T
(2) 计算样本的协方差矩阵 XX ；
(3) 对协方差矩阵 XX 进行特征值分解； 依次选取对模型影响最大的参数调优，直到所有的
T
T
(4) 对协方差矩阵 XX 的特征值计算累计方差贡献率 参数调整完毕。本文中只涉及核参数 C 值的优化，
d ′ / d
∑ ∑
λ i > t； 应用上述方法得到的最优值为45.62。
λ i
√
i=1 i=1 对 k 值在样本量开平方 80 附近进行枚举计
(5) 取 最 大 的 d 个 特 征 值 所 对 应 的 特 征 向 量
′
w 1 , w 2 , · · · , w d ′。 算确定，得到在训练样本中不同 k 值与识别正确率
输出 投影矩阵 W ∗ = {w 1 , w 2 , · · · , w d ′}。 之间的关系如图2所示。
100
这样就可以将一个特征样本 x 映射到一个 d ′
维特征子空间上去，此空间的维度小于原始的 d 维 80
空间： 60

d
x = [x 1 , x 2 , · · · , x d ], x ∈ R , ᝫጷನవ൤ᆸគѿဋ/% 40
↓ xW , W ∈ R d×d ′ , (6) 20
∗
∗
d
′
z = [z 1 , z 2 , · · · , z d ], z ∈ R .
′
0
3 4 5 6 7 8 9 10 11
本文取阈值t = 95%，根据计算确定d = 16，其 k ϙ
′
方差贡献图如图1所示。
图 2 k 值与识别正确率之间的关系
从图 1 可看出，第一主元占方差总和的 22% 左 Fig. 2 The relationship between k and recognition
右，前16个主元占总体方差的95%左右。 accuracy