Page 22 - 201903

304 2019 年 5 月

RAM SNAP 5000 S1
ᇨฉ٨ ᝠካ఻
ᡔܦ฾᧚ጇፒ
40
͜୧ᡰሏ/mm S1
ᛰѓ٨ ஊܸ٨

Ͱᤰ໚ฉ٨
Z
ԍႃᬝၬ PVDF 120
ᡔܦ૱ᑟ٨ θ ೛࿄૱ᑟ٨
Dτ=18.8 µs
0 10 20 30 40 50 60
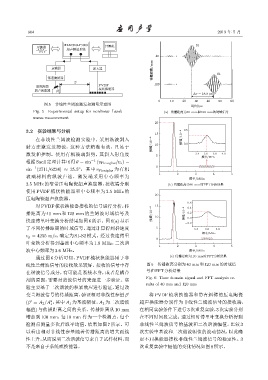
图 5 非线性兰姆波激发和测量示意图
௑ᫎ/µs
Fig. 5 Experimental setup for nonlinear Lamb (a) ͜୧ᡰሏ˞40 mm֗120 mmᄊ௑۫ηՂ
waves measurement
20
3.2 实验结果与分析 0.5
15
在非线性兰姆波检测实验中，采用纵波斜入 ૝ࣨ/10 -4
射方法激发兰姆波，这种方法精准有效，且易于 ૝ࣨ/10 -4 10 0.0
激发和控制。使用有机玻璃斜劈，其斜入射角度 5 3.4 3.6 3.8 4.0
ᮠဋ/MHz
根据 Snell 定理计算可得 θ = sin −1 (v Plexiglas /v s ) =
0
sin −1 (2711/6224) ≈ 25.5 ，其中 v Plexiglas 为有机
◦
1 2 3 4 5
玻璃材料的纵波声速。激发端采用中心频率为
ᮠဋ/MHz
2.5 MHz 的窄带压电陶瓷超声换能器，接收端分别 (b) ͜୧ᡰሏ˞40 mm௑FFTѬౢፇ౧
使用 PVDF 梳状换能器和中心频率为 3.5 MHz 的
20
压电陶瓷超声换能器。
0.6
对PVDF 梳状换能器接收的信号进行分析，传 15 0.4
播距离为 40 mm 和 120 mm 的兰姆波时域信号及 ૝ࣨ/10 -4 10 ૝ࣨ/10 -4 0.2
快速傅里叶变换分析结果如图 6 所示。图 6(a) 显示 0.0
-0.2
了不同传播距离的时域信号，通过计算得到群速度 5 3.4 3.6 3.8
ᮠဋ/MHz
v g = 4255 m/s，确定为 S1-S2 模式。经过快速傅里
0
叶变换分析得到基波中心频率为 1.8 MHz，二次谐
1 2 3 4 5
波中心频率为3.6 MHz。 ᮠဋ/MHz
通过图 6 分析可知，PVDF 梳状换能器用于非 (c) ͜୧ᡰሏ˞120 mm௑FFTѬౢፇ౧
线性兰姆波信号的接收效果较好。接收的信号中存 图 6 传播距离分别为 40 mm 和 120 mm 的时域信
在谐波信号成分，有可能是系统本身，或者是耦合 号和 FFT 分析结果
Fig. 6 Time domain signal and FFT analysis re-
剂的原因，需要对谐波信号的来源进一步验证。实
sults of 40 mm and 120 mm
验主要基于二次谐波的积累效应进行验证，通过改
变兰姆波信号的传播距离，验证相对非线性参量 β ′ 将 PVDF 梳状换能器和带有斜劈的压电陶瓷
2
(β = A 2 /A ，其中 A 1 为基波幅值，A 2 为二次谐波 超声换能器分别作为非线性兰姆波信号的接收端，
′
1
幅值) 与传播距离之间的关系。传播距离从 10 mm 在相同实验条件下进行 3次重复实验，3次实验分别
增加到 100 mm，每 10 mm 作为一个检测点，每个 在不同时间段完成。通过短时傅里叶变换分析得到
检测点测量多次后取平均值，结果如图 7 所示。可 非线性兰姆波信号的基波和二次谐波幅值，比较 3
以看出相对非线性参量随着传播距离的增大而线 次实验中基波和二次谐波幅值的波动情况，以此确
性上升，从而说明二次谐波信号来自于试样材料，而 定不同换能器接收非线性兰姆波信号的稳定性。3
不是来自于系统或换能器。 次重复实验中幅值的变化情况如图8所示。