Page 11 - 应用声学2019年第4期

第 38 卷 第 4 期 尚尔昌： 水声学中地声反演的新进展 471

参数组合所具有的反射性能与真实海底的反射性 2(ρ b /ρ w )
P s = √ , (10)
能相吻合 (注意：这里不是绝对意义上的吻合，只是 1 − (c w /c b ) 2
2
最佳意义上的吻合，只有模型不存在失配时才有绝 (ρ b /ρ w )(c w /c b ) η
Q = 2 2 3/2 , (11)
对一致)。 [1 − (c w /c b ) ]
可见，一组地声参数所反映的声反射特性才是 η = α/2k b , k b = 2πf/c b . (12)
直接影响声场的物理量，也就是说，用声反射特性参 [14]
Harrison 对上述线性近似对传播损失预报
数来描写海底不仅具有实质物理意义，也更具实用
所引起的误差做过分析，结果表明在距离为 30倍水
意义。实际上，匹配场反演采用的一般是远场数据，
深的范围内传播损失的预报误差在1.5 dB左右。
因此得到的是 “小掠射角” 的反射特性，这一点带来
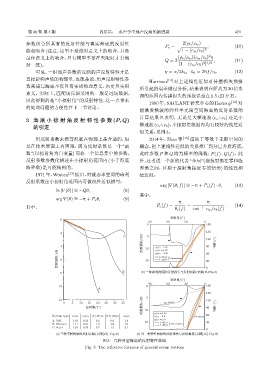
1980 年，SACLANT研究中心的 Hastrup [15] 对
的处理问题的方便性在下一节讨论。
能激发横波的弹性半无限空间海底的反射系数的
计算结果也表明，无论是大横速波 (c s >c b ) 还是小
3 海 底 小 掠 射 角 反 射 特 性 参 数 (P, Q)
横速波(c s <c b )，小掠射角范围内均有较好的线性近
的引进
似关系，见图3。
用反射系数来描写海底在物理上是合适的，但 2014 年， Zhao 等 [16] 借助于等效半无限空间的
是在技术层面上有困难，因为反射系数是一个 “函 概念，把上述线性近似的关系推广到分层介质海底，
数”(以掠射角为自变量) 而非一个信息集中的参数。 此时参数 P 和 Q 均为频率的函数：P(f)、Q(f)。此
反射系数参数化描述在小掠射角范围内 (小于海底 外，还引进一个新的代表“全局”(指掠射角在零和临
临界角)是可能做到的。 界角之间，区别于掠射角接近零的情形) 的线性相
1971年，Weston [13] 提出，对液态半空间的瑞利 位近似：
反射系数在小掠射角范围内可做线性近似描写：
arg |V (θ; f)| = −π + P c (f) · θ, (13)
∼
∼
ln |V (θ)| = −Qθ, (8)
其中，
∼
arg V (θ) = −π + P s θ, (9)
π π
其中， P c (f) = θ c (f) = cos −1 c w /c b (f) . (14)
ଉ࠱ᝈ/(O)
0
90 60 30 0
0 180
2 150
Ԧ࠱૯ܿ/dB ཌྷ၍/(O)
C 5 120
4 10 c ⊳c 1/⊲ 90
c s⊳c 1/⊲
Ԧ࠱૯ܿ/dB 6 15 ρ  ⊳ρ 1 /⊲ Attenuation 60
0 dB/λ
1 dB/λ }
ion
30
0
B C ʷመुভ๒अᄊԦ࠱૯ܿˁԦ࠱ᄱረ ஡࿹< > 'JH
8
ଉ࠱ᝈ/(O)
90 60 30 0
10 0 180
A
150
Ԧ࠱૯ܿ/dB
12 5 120
0 5 10 15 20 25 30 35 No shear
ଉ࠱ᝈ/(O) 10 90 ཌྷ၍/(O)
Bottom type c ⊳c  c s /c 2 (I) dB/λ (II) dB/λ ρ ⊳ρ  c ⊳c 1/⊲ No shear 60
c s ⊳c 1 /⊲
A: Soft 1.03 0.23 0.2 0.6 1.6 15 ρ ⊳ρ 1/⊲ 30
1 dB/λ }
B: Medium 1.11 0.27 1.0 2.0 1.9 0 dB/λ Attenuation
C: Hard 1.24 0.35 0.7 1.5 2.1
0
B ʼመˀՏ๒अᄊԦ࠱ᛰѓ(஡࿹[15] Fig.9) D Գʷመुভ๒अᄊԦ࠱૯ܿˁԦ࠱ᄱረ(஡࿹[15] Fig.8)
图 3 几种典型海底的反射特性曲线
Fig. 3 The reflective features of general ocean bottom