Page 14 - 应用声学2019年第4期

474 2019 年 7 月

0 (3) 在过去数十年的地声反演中，由于模型失
配导致反演的地声参数的畸变，多数反演结果并不
1.0
能反映海底固有地声参数，尤其是海底底质固有衰
减系数α(f)。
2.0 (4) 引进了不基于地声模型的海底反射特性参
ງए/m 数 (P, Q)，为研究海底打开一扇新的窗户，也增加
3.0
了解决海底反演问题的途径。

Real (5) 为克服模型失配带来的反演结果失真，
4.0
Inverted
through P↼f↽ 我们提出两种解决方法：“WKB+P(f)” 方法和
“N×HHS”方法。
5.0
1500 1540 1580 1620
ܦᤴ/(mSs -1 ) 以 SACLANT 海底模型为例进行数值分析，通
过上述两种方法提取海底无畸变的固有衰减系数，
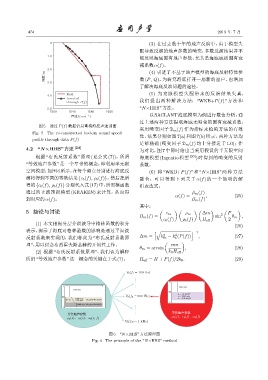
图 5 通过 P(f) 数据信息重构海底声速剖面
采用畸变因子 D m (f) 作为指标来检验方法的有效
Fig. 5 The re-constructed bottom sound speed
性，结果分别如图 7(a) 和图 7(b) 所示，两种方法均
profile through data P(f)
足够精确 (畸变因子 D m (f) 均十分接近于 1.0)；作
4.2 “N×HHS”方法 [24] 为对比，图 7 中同时给出当采用假设的半无限空间
根据 “布氏反射系数” 原理 (见公式 (7))，所谓 海底模型 (Ingenito 模型 [20] ) 时得到的畸变的反射
“等效地声参数” 是一个窄带的概念，即利用半无限 系数。
空间模型，如图 6 所示，在每个频点分别进行海底反 (6) 将 “WKB+P(f)” 和 “N×HHS” 两种方法
演将得到不同的等效结果{c b (f), ρ b (f)}。然后把所 融合，可以得到下列关于 α(f) 的一个简明的解
得的{c b (f), ρ b (f)}分别代入式(17)中，所需模函数 析表达式：
通过简正波预报模型 (KRAKEN) 来计算，从而得 β m (f)
α(f) = , (25)
到对应的α(f)。 B m (f)
其中，
5 结论与讨论 ( c m ) ( ρ w ) ( ∆m ) ( P )
B m (f) = sin 2 θ m ,
c b (f) ρ b (f) H eff 2
(1) 本文根据分层介质波导中格林函数的积分 (26)
表示，揭示了海底对格林函数的影响是通过平面波 [√ ] −1
2
2
反射系数来实现的，我们称此为 “布氏反射系数原 ∆m = k − k (P(f)) , (27)
b
m
( )
理”，用以纪念布烈霍夫斯基赫的开创性工作。 mπ
θ m = arcsin , (28)
(2) 根据 “布氏反射系数原理”，我们认为解释 k 0 H eff
所谓“等效地声参数”这一概念的关键在于式(7)。 H eff = H + P(f)/2k 0 . (29)
V b (f  =100 Hz)

0
0
1500 m/s
1500 m/s
100
ρ=1.6 g/cm 3
V b (f  =500 Hz) c=1550 m/s
100
1520 m/s α=0.35 dB/λ
2.5 m 1580 m/s 1.6 g/cm 3 0.3 dB/λ
z
1600 m/s 1.8 g/cm 3 0.4 dB/λ
z
ᄾࠄڡܦԠ஝ ኎஍ڡܦԠ஝
ρ b ↼z↽ǃc b ↼z↽ǃα b ↼z f↽ ρ b ↼f↽ǃc b ↼f↽ǃα b ↼f↽
V b(f N=1 kHz)
图 6 “N×HHS” 方法原理图
Fig. 6 The principle of the “N×HHS” method