Page 277 - 应用声学2019年第4期

第 38 卷 第 4 期 郭政等： 基于变分模态分解和对称相关的目标舰船线谱检测 737

1.0 考查处理前后线谱成分之外的部分，定义
ᄱТጇ஝
2
2
r/⊲ y = n /T，给出y 的概率密度：
0.8
1 yT /2σ ′2
K(y) = √ 2πyσ n /T e n , (17)
0.6
ᄱТጇ஝ 0.4 于是 y 的平均功率为 2σ /T 。则第二步处理后的
′
′ 4
2
信噪比为 n
0.2
( )
N 4
1 ∑ A
SNR out2 = 10 lg n , (18)
0 ′ 4 2 8
0 2 4 6 8 10 2σ /T n=1
n
BIMF᫽஝
因此，第二步的处理增益可以写为
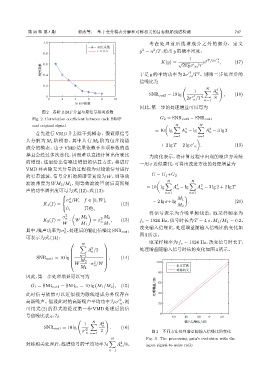
图 2 各阶 BIMF 分量与原信号相关系数
Fig. 2 Correlation coefficient between each BIMF G 2 = SNR out2 − SNR out1
and original signal ( ∑ ∑
N
N
= 10 lg A − lg A − 3 lg 2
2
4
首先进行 VMD 并去除干扰模态。假设原信号 n n
n=1 n=1
共分解为 M 1 阶模态，其中共有 M 2 阶为包含线谱 )
′
+ 2 lg T − 2 lg σ n . (19)
成分的模态。由于 VMD 结果依赖于多项参数的选
择且会经过多次迭代，因而难以直接计算出信噪比 为简化表示，将计算过程中出现的噪声方差统
的增量，这里给出信噪比增量的估算方法：将进行
一用σ 近似替代，可得出改进方法的处理增益为
VMD 并去除无关分量的过程视为对线谱信号进行
的窄带滤波，信号分析的频谱带宽设为 W，则等效 G = G 1 +G 2
N
N
滤波带宽为 WM 2 /M 1 ，则等效滤波 [3] 前后高斯噪 ( ∑ ∑
2
4
= 10 lg A − lg A − 3 lg 2 + 2 lg T
声的功率谱密度可写为式(12)、式(13)： n n
n=1 n=1

)
 2 − 2 lg σ+ lg M 1 (20)
σ /W, f ∈ [0, W],
K 1 (f) = n (12) M 2 .
0, 其他,

将信号表示为含噪单频线谱，取采样频率为
(
)
σ n 2 M 2 2 M 2
K 2 (f) = · W = σ n , (13) f s = 1024 Hz，信号时长为 T = 4 s，M 1 /M 2 = 0.2。
W M 1 M 1
改变输入信噪比，处理增益随输入信噪比的变化如
2
其中，噪声功率为σ 。处理后的输出信噪比SNR out1
n
可表示为式(14)： 图3所示。
取采样频率为 f s = 1024 Hz，改变信号时长 T，
 
N
∑ 2
A /2 处理增益随输入信号时长的变化如图4所示。
 n 
 n=1 
SNR out1 = 10 lg   , (14)
 M 2  100
W · σ /W వ஡வข
 2 
n
M 1
ࠫሦᄱТ
80
因此，第一步处理增益可以写为
( ) 60
G 1 = SNR out1 − SNR in = 10 lg M 1 /M 2 , (15) ܫေܙᄞ/dB
此时信号依然可以近似视为除线谱成分外仅存在 40
′ 2
高斯噪声。假设此时的高斯噪声平均功率为σ ，则
n 20
可用式 (2) 的形式将经过第一步 VMD 处理后的信
号信噪比表示为 0 -60 -40 -20 0 20
( )
N 2 ᣥКη٪උ/dB
1 ∑ A
SNR out1 = 10 lg n . (16)
σ ′ 2 2 图 3 不同方法处理增益随输入信噪比的变化
n n=1
N Fig. 3 The processing gain’s evolution with the
∑
4
对称相关处理后，线谱信号的平均功率为 A /8。 input signal-to-noise ratio
n
n=1