Page 45 - 应用声学2019年第4期

第 38 卷 第 4 期 张永霖等： 基于混合范数约束的非均匀稀疏水声信道估计方法 505

定义如式 (17) 所示的均方误差 (Mean-square
3 仿真实验
error, MSE)参数为性能评价标准，
M
为了考察本文提出算法的优越性，通过仿真实 1 ∑
2
MSE = 10 lg (ω i − h i ) . (17)
验与标准 APA 算法、l 1 范数约束 APA 以及均匀分 M
i=1
组l 21 -IPAPA进行性能对比分析。
仿真中各算法针对相同的仿真稀疏信道 h 进
本文采用 BELLHOP 水声信道仿真模型进行 行估计得到 ω，取信道估计误差的欧式范数作为评
簇稀疏水声信道构建，设置一个发射源和一个接
价的标准，其中 M 为滤波器长度。本文对 4 种算法
收端，深度分别为 500 m 和 600 m，距离 50 km，水
的收敛速度以及稳态误差进行对比仿真研究，由自
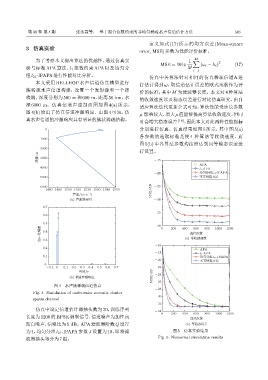
深 6000 m。仿真信道声速剖面图如图 4(a) 所示， 适应算法迭代更新公式可知，算法性能受步长参数
图 4(b) 给出了仿真信道冲激响应。由图 4 可知，仿
µ 影响较大，增大 µ值能够提高算法收敛速度，但同
真水声信道的冲激响应具有明显的簇状稀疏结构。
时会增大稳态误差 [18] ，因此本文对此两种性能指标
0 分别进行仿真。仿真结果如图 5 所示，其中图 5(a)
各参数的选取标准是使 4 种算法等收敛速度，而
1000
图 5(b) 中各算法参数均按照达到同等稳态误差进
2000 行设置。
ງए/m 3000 -15

APA
4000
l  -APA
-20 کӉѬጸl -IPAPA
5000 వ஡ਫ਼ଢவข
6000 -25
1480 1490 1500 1510 1520 1530 1540 1550 MSE/dB
ܦᤴ/(mSs -1 )
(a) ܦᤴҖ᭧ڏ -30
0.7
-35
0.6
0.5 -40 0 200 400 600 800 1000 1200
ॆʷӑࣨए 0.4 (a) ኎ஆகᤴए
ᤖ̽൓஝
0.3
-16
0.2
APA
-18 l  -APA
0.1 کӉѬጸl  -IPAPA
-20 వ஡ਫ਼ଢவข
0
-0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 -22
MSE/dB -24
௑ण/s
(b) η᥋ф༏־ऄ
图 4 水声簇稀疏信道仿真 -26
-28
Fig. 4 Simulation of underwater acoustic cluster
-30
sparse channel
-32
仿真中设定信道估计器抽头数为 70，训练序列 -34
0 200 400 600 800 1000 1200
长度为 1200的BPSK调制信号，信道噪声为加性高 ᤖ̽൓஝
斯白噪声，信噪比为5 dB。APA滤波器阶数Q 设置 (b) ኎ሷগឨࣀ
为 4，均匀分组 l 21 -IPAPA 参数 J 设置为 10，即将滤 图 5 仿真实验结果
波器抽头等分为7组。 Fig. 5 Numerical simulation results