Page 83 - 应用声学2019年第4期
P. 83
第 38 卷 第 4 期 毛卫宁等: 一种低复杂度的稳健自适应波束形成 543
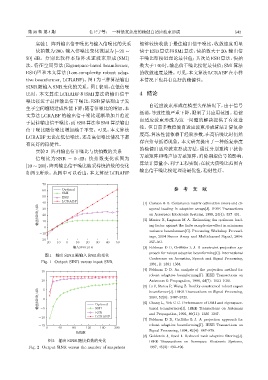
实验1 阵列输出信干噪比与输入信噪比的关系 能够较快收敛于最佳输出信干噪比,收敛速度明显
快于 ESB 算法和 SMI 算法,快拍数大于 20,输出信
快拍数为 200,输入信噪比变化范围为 [−20 ∼
50] dB。分别比较样本矩阵求逆波束形成 (SMI) 干噪比即接近理论最佳值;其次是 ESB 算法,快拍
法、特征空间算法 (Eigenspace-based beamformer, 数大于 140时,输出信干噪比接近最佳值;SMI 算法
ESB) [3] 和本文算法 (Low-complexity robust adap- 的收敛速度最慢。可见,本文算法 LCRABF在小样
tive beamformer, LCRABF)。图1为三种算法输出 本情况下也具有良好的稳健性。
SINR随输入SNR变化的关系。图1表明,在低信噪
比时,本文算法 LCRABF 和 SMI 算法的输出信干 4 结论
噪比接近于最佳输出信干噪比,ESB 算法则由于发
自适应波束形成在模型失配情况下,由于信号
生子空间缠绕造成性能下降;随着信噪比的增加,本
抵消,导致性能严重下降,限制了其应用范围。稳健
文算法 LCRABF 的输出信干噪比逐渐增加且趋近
自适应波束形成为这一问题的解决提供了有效途
于最佳输出信干噪比,而ESB算法和 SMI算法输出
径。但目前多数稳健自适应波束形成算法计算复杂
信干噪比随信噪比增加趋于不变。可见,本文算法
度高,算法性能依赖于经验参数,在高信噪比时仍然
LCRABF无论在低信噪比,还是高信噪比情况下都
存在信号抵消现象。本文研究提出了一种低复杂度
有良好的稳健性。
的稳健自适应波束形成方法,通过分别重构干扰协
实验2 阵列输出信干噪比与快拍数的关系
方差矩阵和噪声协方差矩阵,消除期望信号的影响,
信噪比为 SNR = 0 dB;快拍数变化范围为
算法计算量小,利于工程实现;在较大信噪比范围内
[10 ∼ 200],阵列输出信干噪比随采样快拍数的变化
输出信干噪比接近理论最优值,稳健性好。
如图 2 所示。从图中可以看出,本文算法 LCRABF
70
60 Optimal 参 考 文 献
SMI
50 ESB
LCRABF
40 [1] Carlson B D. Covariance matrix estimation errors and di-
ᣥѣSINR/dB 20 [2] Mestre X, Lagunas M A. Estimating the optimum load-
agonal loading in adaptive arrays[J]. IEEE Transactions
30
on Aerospace Electronic Systems, 1988, 24(4): 397–401.
10
0 ing factor against the finite sample size effect in minimum
variance beamformers[C]. Processing Workshop Proceed-
-10
ings, 2004 Sensor Array and Multichannel Signal, 2004:
-20
-20 -10 0 10 20 30 40 50 357–361.
ᣥКSNR/dB [3] Feldman D D, Griffiths L J. A constraint projection ap-
proach for robust adaptive beamforming[C]. International
图 1 输出 SINR 随输入 SNR 的变化
Conference on Acoustics, Speech and Signal Processing,
Fig. 1 Output SINR versus input SNR
1991, 2: 1381–1384.
[4] Feldman D D. An analysis of the projection method for
15
robust adaptive beamforming[J]. IEEE Transactions on
10 Antennas & Propagation, 1996, 44(7): 1023–1030.
[5] Li J, Stoica P, Wang Z. Doubly constrained robust capon
ᣥѣSINR/dB 0 Optimal [6] Chang L, Yeh C C. Performance of DMI and eigenspace-
5
beamformer[J]. IEEE Transactions on Signal Processing,
2004, 52(9): 2407–2423.
-5
SMI
ESB based beamformers[J]. IEEE Transactions on Antennas
and Propagation, 1992, 40(11): 1336–1347.
-10 LCRABF
[7] Feldman D D, Griffiths L J. A projection approach for
-15 robust adaptive beamforming[J]. IEEE Transactions on
0 40 80 120 160 200
Signal Processing, 1994, 42(4): 867–876.
ঌથ
[8] Goldstein J, Reed I. Reduced rank adaptive filtering[J].
图 2 输出 SINR 随快拍数的变化 IEEE Transactions on Aerospace Electronic Systems,
Fig. 2 Output SINR versus the number of snapshots 1997, 45(2): 492–496.