Page 38 - 应用声学2019年第5期

790 2019 年 9 月

c γ m 为相应波型在第 m 层介质中的群速度。M m 束，利用其主轴上的声场来近似每一点的球面波，即
γ m
m
为 2 × 2 的矩阵，与每一层介质的密度和声速有关， 通过旋转高斯声束，使空间中所有场点均位于主轴
可以利用ABCD 矩阵法计算得出 [10] 上，如此，既可以利用高斯声束在多层介质中的传播
[ G G ] 特性，又能准确地求出各场点的声场幅值。因此，第
γ m
M m (s m ) = D M 1 γ 1 (0) + C
[ G G ] −1 n 个阵元在第 M+1 层介质中产生的质点速度幅值
× A + B M γ 1 (0) , (2)
1 可表示为 [14]
其中， γ M+1 ;n
v (ω)
  M+1
A G B G  √ [ ( )]
Q  det M q,γ M+1 s q,γ M+1
  ∑ q q,γ M+1 M+1 M+1
C G D G = v 0 A D d √
R M+1
 [ q,γ M+1 ]
q=1 det M (0)
    M+1
γ M+1 ;p γ M+1 ;p γ M ;t γ M ;t
A M+1 B M+1 A M B M [ √ ]
=  γ M+1 ;p γ M+1 ;p    m=M γ m ;γ m+1 det [M m (s m )]
q,γ m
q,γ m
∏
C D C γ M ;t D γ M ;t × T m,m+1 √
M+1 M+1 M M q,γ m (0)]
m=1 det [M m
   
γ M ;p γ M ;p γ 1 ;p γ 1 ;p [ ]}
A M B M A 1 B 1 M+1 q,γ m
∑
×   · · ·   , (3) × exp iω s m , (7)
C γ M ;p D γ M ;p C γ 1 ;p D γ 1 ;p c m
γ m
M M 1 1 m=1
  
 1 0 其中，v 0 表示阵元表面振动幅值，Q 表示阵元离散

 γ m ;p γ m ;p
A m = D m = I =   , 单元个数，D R 为单个小单元的声场辐射指向性函


 0 1
(4) [14]
  数 。
 0 0

B m = c γ m s m I, C m =O=   , 1.2 射线追踪法计算声波路径及时间延迟
 γ m ;p γ m ;p

m

0 0

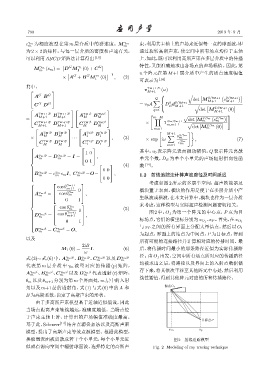
考虑如图 2 所示的多层半空间，超声换能器及
  γ m+1 
cos θ
 m+1
 0 楔块置于表面，楔块的作用是便于在多层介质中产
 γ m ;t  γ m 
A =  cos θ m  ,

 m
 生纵波或横波，在本文计算中，楔块也作为一层介质

 0 1


 来考虑，这种模型与实际超声检测问题密切相关。
 
cos θ γ m
m 0 (5)
 γ m ;t  cos θ γ m+1  图 2 中，O 1 为第一个阵元的中心点，P 点为目
D m+1  ,

 m = 


 0 1 标场点，它们的横坐标分别为x O 1 、x P 。首先，在x O 1



 与 x P 之间的所有界面上分配大量结点，然后以 O 1
 γ m ;t γ m ;t
B m = C m = O,
为起点，界面上的结点为中间点，P 为目标点，得到
以及
所有可能的连接路径并计算相对应的传播时间。最
2iB
M 1 (0) = I. (6) 后，将传播时间最小的那条路径近似为实际传播路
ω
径。由O 1 出发，空间中所有场点所对应的传播路径
γ m ;p
式 (3)∼ 式 (6) 中，A γ m ;p 、B γ m ;p 、C m 以及 D γ m ;p
m
m
m
代表第 m 层介质中 γ m 波型对应的传播 (p) 矩阵， 均被求出之后，将路径以及界面上的入射点数据储
存下来，将其依次平移至其他阵元中心处，然后利用
γ m ;t
γ m ;t
γ m ;t
γ m ;t
A 、B 、C 以及 D 代表透射 (t) 矩阵，
m m m m
θ m 以及 θ m+1 分别为第 m 个界面处，m 层中的入射 线性插值，得到其他阵元对应的所有传播路径。
角以及 m+1 层的透射角，式 (1) 与式 (6) 中的 A 和 ູགO 
B 为高斯系数，决定了高斯声束的形状。
由于多高斯声束模型基于近轴近似假设，因此
当场点距离声束轴线越远，准确度越低。当场点位
于声束主轴上时，计算出的声场幅值准确度最高。
ᄬಖགP
基于此，Schmerr [14] 结合点源叠加法以及高斯声束
模型，提出了高斯声束等效点源模型。根据此模型， x O  x p
换能器表面被离散成若干个小单元，每个小单元近 图 2 射线追踪模型
似成点源向空间中辐射球面波，选择特定的高斯声 Fig. 2 Modeling of ray tracing technique