Page 107 - 《应用声学》2019年第6期

第 38 卷 第 6 期 王全东等： 基于深度神经网络的水声信号恢复方法研究 1009

为 32。训练 IRM 时，α 为 0.05。为检验算法降噪和 作为对比，采用水声环境下常用的 CBF 对阵列数
保真的效果，采用两种客观描述参数。 据进行处理。常规波束形成算法流程简述如下：首
先根据阵列位置和俯仰角扫描范围 (0 ∼ 180 ) 确
◦
◦
500
定阵列流形向量，然后利用较高频段的接收数据
-20
400
(300∼500 Hz) 来进行波束扫描，从而获得每一帧信
-40 号的扫描方位谱(接收协方差矩阵利用21个快拍来
ᮠဋ/Hz -60 进行估计)，根据方位谱峰值所在的位置确定每一帧
300
200
接收信号的俯仰角，并据此进行常规波束形成获得
-80
100
输出波形和功率谱。本文的俯仰角的零度定义为垂
-100
0 直向上方向。
500 1000 1500 2000
௑ᫎ/s 作为测试示例，0 dB 带噪测试信号的对数功
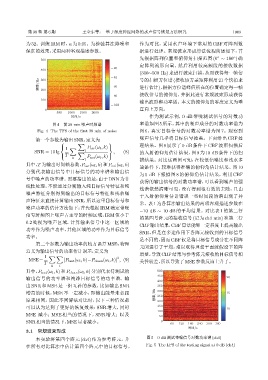
图 4 前 38 min 噪声时频谱 率谱如图 5 所示，其中的噪声成分的对数功率谱为
Fig. 4 The TFS of the first 38 min of noise 图 6，真实目标信号的对数功率谱为图 7。观察到
第一个参数为输出SNR，定义为 噪声信号几乎将目标信号掩盖。下面给出 CBF 处
 ∑ 
理结果。图 8 展示了 0 dB 条件下 CBF 波束扫描后
 1 ∑ P tar (ω l , k) 
SNR = 10 lg ∑ l , (8) 的入射俯仰角估计结果，图 9 为 10 dB 条件下的扫
T P noi (ω l , k) 
k
l 描结果。对比这两图可知，在较低信噪比和浅水多
其中，T 为输出时间帧总数，P tar (ω l , k)和P noi (ω l , k)
途条件下，较难获得准确的俯仰角估计结果。图 10
分别代表输出信号中目标信号的功率谱和输出信
为 0 dB 下根据图 8 的俯仰角估计结果，利用 CBF
号中噪声的功率谱。需要指出的是，由于DNN为非
获得的输出信号的对数功率谱，可以看到噪声的强
线性处理，不能通过分别输入纯目标信号特征和纯
线谱依然清晰可见，没有得到很有效的去除，且由
噪声特征分别得到输出的目标信号特征和残余噪
于入射俯仰角估计错误一些时间段的谱出现了异
声特征来直接计算输出 SNR，所以这里目标信号和
常。表 1 为各算法输出结果的两项客观描述参数在
噪声功率的估计方法如下：首先根据IRM 确定带噪
−10 dB ∼ 10 dB 的平均结果。对比表 1 的第二行
信号时频图上噪声占主导的时频区域，IRM 值小于
的第四号阵元的接收信号 (记为 ch4 mix) 和第三行
0.2 处视为噪声区域，计算输出信号中这一区域的
CBF输出结果，CBF算法能够一定程度上提高输出
功率作为噪声功率，其他区域的功率作为目标信号
SNR，但是在多途作用下各阵元接收到的目标信号
功率。
是不同的，因而CBF仅是将目标信号成分在不同阵
第二个参数为输出功率的均方误差MSE，物理
元间进行了平均，难以取得理想平面波假设下的阵
意义为输出信号的功率估计误差，定义为
1 ∑ ∑ 2 增益，导致CBF 结果与参考阵元接收的目标信号相
MSE= [P test (ω l , k)−P clean (ω l , k)] , (9) 关性较差，所以导致了MSE参数反而上升了。
T
k l
其中，P test (ω l , k) 和 P clean (ω l , k) 分别代表待测试的 500
450
输出信号的功率谱和纯净目标信号的功率谱。输 20
400
出 SNR 和 MSE 是一组互补的参数，比如输出 SNR 350
增高的时候，MSE 不一定减小，即输出能量未必跟 ᮠဋ/Hz 300 15
250
原来相同。因此不同算法对比时，以下三种情况都 200
可以认为达到了更好的恢复效果：SNR 增大，同时 150 10
100
MSE 减小；MSE 相当的情况下，SNR 增大；以及 50
SNR相当的情况下，MSE显著减小。 0
60 120 180 240 300 360
௑ᫎ/s
3.1 常规波束形成
本实验将第四个阵元 (ch4) 作为参考阵元，并 图 5 0 dB 测试带噪信号对数功率谱 (ch4)
在所有对比算法中估计第四个阵元中的目标信号。 Fig. 5 The LPS of the testing signal at 0 dB (ch4)