Page 110 - 《应用声学》2019年第6期

1012 2019 年 11 月

噪后的特征一同送入 DNN 本质上提高了训练的丰 70
富度，因此融合 DNN 能从中学习并将第一阶段没 60
有处理好的时频点进一步恢复。
50
500 40 CBFᣥѣࠫ஝MSE
450 20 ࠫ஝MSE ӭ᫼ЋDNNᣥѣࠫ஝MSE
400 30 ː᫽඀DNNᣥѣࠫ஝MSE
350 20
ᮠဋ/Hz 250 15 10
300
200
0
150 -10 -5 ᣥКSNR/dB 5 10
10
100
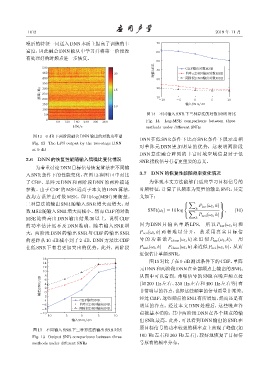
50 图 14 不同输入 SNR 下三种算法的对数 MSE 对比
0 Fig. 14 Log-MSE comparisons between three
60 120 180 240 300 360
௑ᫎ/s methods under different SNRs
图 12 0 dB 下两阶段融合 DNN 输出的对数功率谱
DNN 在低 SNR 条件下比高 SNR 条件下展示出相
Fig. 12 The LPS output by the two-stage DNN
对单阵元 DNN 更加明显的优势，这表明两阶段
at 0 dB
DNN 算法融合阵列的丰富时域空域信息对于低
3.6 DNN的恢复性能随输入信噪比变化情况 SNR接收信号有着更重要的意义。
为着重讨论 DNN 目标信号恢复算法在不同输
入 SNR 条件下的性能变化，在图 13 和图 14 中对比 3.7 DNN的恢复性能随频率变化情况
了 CBF、单阵元 DNN 和两阶段 DNN 的两种描述 为体现本文方法能够自适应学习目标信号的
参数。由于 CBF 的 MSE 远高于本文的 DNN 算法， 时频特征，计算了以频率为变量的输出 SNR，其定
故均方误差由对数 MSE，即 10 log(MSE) 来衡量。 义如下：
三种算法的输出 SNR 随输入 SNR 增大而增大，对  ∑ 
 P tar (ω l , k) 
数MSE随输入SNR增大而减小。然而CBF的对数 SNR(ω l ) = 10 log ∑ k , (10)
 P noi (ω l , k) 
MSE 始终高出 DNN 输出结果 30 以上，说明 CBF k
的功率估计远不及 DNN 准确。随着输入 SNR 增 因 为 DNN 只 输 出 单 路 LPS， 所 以 P tar (ω l , k) 和
大，两阶段 DNN 的输出 SNR 与 CBF 的输出 SNR P noi (ω l , k) 两 者 难 以 分 开， 故 采 用 真 实 目 标 信
的差距从 10 dB 减小到了 2 dB，DNN 方法比 CBF 号 的 功 率 谱 P clean (ω l , k) 来 近 似 P tar (ω l , k)， 用
在低 SNR 下有着更加突出的优势。此外，两阶段 P test (ω l , k) − P clean (ω l , k) 来近似 P noi (ω l , k)，从而
近似估计单频SNR。
16 图 15 对比了在 0 dB 测试条件下的 CBF、单阵
14
12 元 DNN 和两阶段 DNN 在全部频点上输出的 SNR。
10
8 6 从图中可以看到，带噪信号的 SNR 在噪声频点处
ᣥѣSNR/dB 4 2 (如 200 Hz 左右、350 Hz 左右和 400 Hz 左右等) 有

非常明显的谷点，也即这些频率的信号质量非常差。
-2 0 经过 CBF，这些频点的 SNR 有所增加，然而还是有
-4 CBFᣥѣSNR
-6 ӭ᫼ЋDNNᣥѣSNR 明显的谷点。经过本文 DNN 处理后，这些噪声谷
-8 ː᫽඀DNNᣥѣSNR
-10 点被基本消除，其中两阶段 DNN 在各个频点的输
-10 -5 0 5 10
ᣥКSNR/dB 出 SNR 最高。此外，可以看到 DNN 输出的 SNR 在
原目标信号的功率较强的频率点上出现了峰值 (如
图 13 不同输入 SNR 下三种算法的输出 SNR 对比
100 Hz 左右和 360 Hz 左右)，较好地恢复了目标信
Fig. 13 Output SNR comparisons between three
methods under different SNRs 号原有的频率分布。