Page 111 - 《应用声学》2019年第6期
P. 111
第 38 卷 第 6 期 王全东等: 基于深度神经网络的水声信号恢复方法研究 1013
30
ࣜ٪ηՂ 4 结论
CBF
20 ӭЋDNN 本文提出了一种基于 DNN 的水声目标信号被
ᣥѣSNR/dB 10 动恢复方法。DNN 作为回归模型,具有强大的建模
ːDNN
0 能力,建立了带噪对数功率谱特征到纯净对数功率
谱特征的多维映射函数。本方法在单阵元下利用时
间和频谱信息恢复了目标信号,并利用多目标训练
-10
提高了鲁棒性;在接收阵情况下采用阵元 DNN 同
100 200 300 400 500
ᮠဋ/Hz 时将阵列信号映射到参考阵元,提高了空域信息利
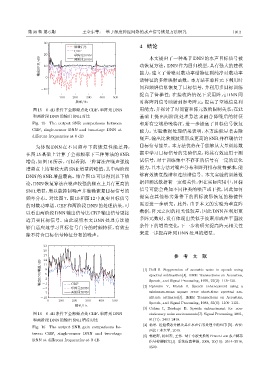
图 15 0 dB 条件下全部频点处 CBF、单阵元 DNN 用能力,并探讨了时间窗和阵元数的限制关系;在此
和两阶段 DNN 的输出 SNR 对比 基础上提出两阶段处理算法来融合降噪后的特征
Fig. 15 The output SNR comparisons between 和所有空域带噪特征,进一步提高了目标信号恢复
CBF, single-sensor DNN and two-stage DNN at 能力。实验数据处理结果表明,本方法能显著去除
different frequencies at 0 dB
噪声,输出比常规波束形成更高的SNR并准确估计
为体现 DNN 在不同频率下的恢复性能差异, 目标信号能量。本方法优势在于能够从大量训练数
在图 15 基础上计算了全部频率下三种算法的 SNR 据中学习目标信号的先验信息,将其有效应用于测
增益,如图16所示。可以看到,三种算法在噪声强线 试信号,对于训练集中不存在的信号有一定的泛化
谱频点上均有较大的 SNR增益的峰值,其中两阶段 能力,且本方法对噪声分布和阵列排布没有要求,能
DNN的SNR增益最高。结合图 15可以得到以下结 够有效恢复线谱和连续谱信号。本文实验的训练数
论,DNN恢复算法在噪声较强的频点上具有更高的 据和测试数据有一定相关性,但在实际应用中,目标
SNR增益,所以能抑制噪声并准确恢复目标信号的 信号可能会叠加不同种类的噪声或干扰,因此如何
频率分布。对比图 7、图 10 和图 12 中真实目标信号 提高在其他恶劣条件下的目标波形恢复的稳健性
的对数功率谱、CBF和两阶段DNN的处理结果,可 需要进一步研究。此外,由于本文的实验为垂直阵
以看出两阶段DNN输出信号比CBF输出信号更接 数据,阵元之间的相关性较差,因此 DNN 在利用更
近真实目标信号。由此说明本文 DNN 处理方法能 多阵元数时,没有体现出类似于波束形成在平面波
够自适应地学习目标信号自身的时频特征,有效去 条件下的增益变化,下一步将研究提高阵元相关性
除不符合目标信号特征分布的噪声。 来进一步提高阵列DNN处理的增益。
23
20
17 参 考 文 献
14
ᣥѣSNRܙᄞ/dB 11 8 5 2 [1] Boll S. Suppression of acoustic noise in speech using
spectral subtraction[J]. IEEE Transactions on Acoustics,
Speech, and Signal Processing, 1979, 27(2): 113–120.
-1
-4 CBF [2] Ephraim Y, Malah D. Speech enhancement using a
ӭЋDNN
-7 ːDNN minimum-mean square error short-time spectral am-
-10 plitude estimator[J]. IEEE Transactions on Acoustics,
0 100 200 300 400 500
Speech, and Signal Processing, 1984, 32(6): 1109–1121.
ᮠဋ/Hz
[3] Cohen I, Berdugo B. Speech enhancement for non-
图 16 0 dB 条件下全部频点处 CBF、单阵元 DNN stationary noise environments[J]. Signal Processing, 2001,
和两阶段 DNN 的输出 SNR 增益对比 81(11): 2403–2418.
[4] 杨宏. 经验模态分解及其在水声信号处理中的应用 [D]. 西安:
Fig. 16 The output SNR gain comparisons be-
西北工业大学, 2015.
tween CBF, single-sensor DNN and two-stage
[5] 韩建辉, 杨日杰, 王伟. 基于小波变换的 Power-Law 水声瞬态
DNN at different frequencies at 0 dB 信号检测研究 [J]. 系统仿真学报, 2008, 20(13): 3514–3516,
3520.