Page 21 - 《应用声学》2019年第6期

第 38 卷 第 6 期 丁建策等： 基于稀疏表示和特征加权的离格双耳声源定位 923

从图 3 中可以看出， 在不同的噪声环境下， 3.3 不同混响环境下的双耳声源定位实验
WWSBL-OGBSSL 算法对在格声源的方位角估计 本 小 节 通 过 仿 真 实 验 测 试 了 WWSBL-
准确率比 OC 算法和 IMF 算法高出 3%∼15%，对 OGBSSL 算法在不同混响条件下的方位角估计性
离格声源的方位角估计准确率比 OC 算法和 IMF 能。双耳信号是由不同混响条件下的双耳房间脉冲
算法高出 5%∼20%。特别是在信噪比为 0 dB 时， 响应(Binaural room impulse responses, BRIRs)卷
WWSBL-OGBSSL 算法对在格声源和离格声源的 积纯净语音信号生成。不同混响条件下的BRIRs是
方位角估计准确率分别比 OC 算法和 IMF 算法高 由 MIT HRTF 数据库中的 HRIRs 经镜像法 [21] 模
出15%和20%左右。值得注意的是，OC算法和IMF 拟生成。混响时间分别设定为100 ms到600 ms，间
算法对离格声源的最小估计误差为 5 ，WWSBL- 隔为100 ms。本实验中在格双耳信号的声源方位角
◦
OGBSSL 算法对离格声源的最小估计误差理论上 为−30 ，离格双耳信号的声源方位角为25 。图 4给
◦
◦
可达到 0 。WWSBL-OGBSSL 算法基于 BCDR 特 出了不同混响条件下三种算法对在格声源和离格
◦
征对各个频点进行加权，将扩散场噪声占主要成 声源的方位角估计准确率。
分的频点去除，降低扩散噪声对方位角估计性能
100
的影响，有效提高了双耳声源方位角估计准确 OC(on-grid)
率；同时 WWSBL-OGBSSL 算法基于各频点信号 80 IMF(on-grid)
வͯᝈͥᝠюᆸဋ/%
Proposed(on-grid)
能量优化模型参数，能量强的频点具有更大的权
重，从而进一步提高了噪声环境下的方位角估计 60
准确率。 40

OC(on-grid)
100
IMF(on-grid) 20
Proposed(on-grid) 100 200 300 400 500 600
வͯᝈͥᝠюᆸဋ/% 60 100 (a) ښಫܦູ
80
ຉ־௑ᫎ/ms

OC(off-grid)
40
IMF(off-grid)
80
வͯᝈͥᝠюᆸဋ/%
Proposed(off-grid)
20
30 20 10 0
η٪උ/dB 60
(a) ښಫܦູ 40
OC(off-grid)
100
IMF(off-grid) 20
Proposed(off-grid) 100 200 300 400 500 600
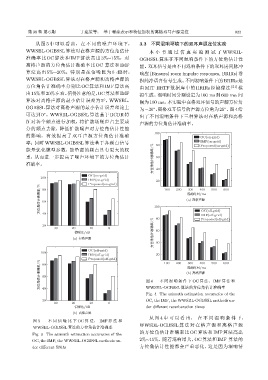
வͯᝈͥᝠюᆸဋ/% 60 图 4 不 同 混 响 条 件 下 OC 算 法、IMF 算 法 和
80
ຉ־௑ᫎ/ms
(b) ሏಫܦູ

WWSBL-OGBSSL 算法的方位角估计准确率
40
Fig. 4 The azimuth estimation accuracies of the
20 OC, the IMF, the WWSBL-OGBSSL methods un-
30 20 10 0
η٪උ/dB der different reverberation times
(b) ሏಫܦູ
从 图 4 中 可 以 看 出， 在 不 同 混 响 条 件 下，
图 3 不 同 信 噪 比 下 OC 算 法、 IMF 算 法 和
WWSBL-OGBSSL 算法对在格声源和离格声源
WWSBL-OGBSSL 算法的方位角估计准确率
的方位角估计准确率比 OC 算法和 IMF 算法高出
Fig. 3 The azimuth estimation accuracies of the
OC, the IMF, the WWSBL-OGBSSL methods un- 2%∼15%。随着混响增大，OC 算法和 IMF 算法的
der different SNRs 方位角估计性能都会严重恶化，这是因为混响情