Page 22 - 《应用声学》2019年第6期

924 2019 年 11 月

况下，由于房间反射，在格双耳信号和离格双耳 方 位 角 间 隔 为 5 。 在 每 个 方 位 角 处， 随 机 选
◦
信号的双耳特征 (ILD、ITD 等) 与自由场环境测 取 TIMIT 数据库的 200 句语音信号作为声源信
˜
量的 HRTF 数据库中提取的双耳特征严重不匹配。 号，采集 200 句双耳信号。假设 θ = {−90 , −80 ,
◦
◦
WWSBL-OGBSSL 算法基于 BCDR 对各个频点的 · · · , 80 , 90 } 为 HRTF 数据库中所有的测量方位
◦
◦
{
双耳信号进行加权，将混响占主要成分的频点去 角，那么当声源真实方位角 θ ∈ − 90 , −80 , · · · ,
◦
◦
}
◦
除，有效降低了混响对方位角估计性能的影响；而 80 , 90 ◦ 时，声源为在格声源，当声源真实方位
◦
◦
◦
◦
且 WWSBL-OGBSSL 算法基于各频点的能量对各 角 θ ∈ {−85 , −75 , · · · , 75 , 85 } 时，声源为离格
个参数迭代更新，能量强的频点会有更大的权重，因 声源。将每个双耳信号划分为时长为 1 s 的双耳
此在混响条件下 WWSBL-OGBSSL 算法的方位角 信号数据段，然后分别采用 OC 算法、IMF 算法
估计性能更优。 和WWSBL-OGBSSL算法估计每段信号的方位角。
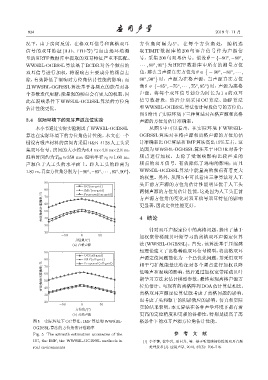
图5 给出了实际环境下三种算法对在格声源和离格
3.4 实际环境下的双耳声源定位实验 声源的方位角估计准确率。
本小节通过实际实验测试了WWSBL-OGBSSL 从图 5 中可以看出，在实际环境下 WWSBL-
算法在实际环境下的方位角估计性能。本文在一个 OGBSSL 算法对在格声源和离格声源的方位角估
铺设有吸声材料的房间内采用 B&K 4128人工头采 计准确率比OC算法和IMF算法高出15%左右。这
集双耳信号。房间的大小约为6.4 m×4.8 m×2.8 m， 是因为 WWSBL-OGBSSL 算法基于 BCDR 对各个
混响时间约为 T 60 ≈ 350 ms，混响半径 r 0 ≈ 1.60 m。 频点进行加权，去除了受混响影响比较严重的
声源位于人工头的水平面上，距人工头的距离为 频点的双耳信号，有效降低了混响的影响；而且
1.80 m，真实方位角分别为{−90 , −85 , · · · , 85 , 90 }， WWSBL-OGBSSL 算法中能量高的频点有着更大
◦
◦
◦
◦
的权重。另外，从图 5 中可以看出三种算法对人工
90 头正前方声源的方位角估计性能明显优于人工头
OC(on-grid)
80 IMF(on-grid) 两侧声源的方位角估计性能，这是因为人工头正前
வͯᝈͥᝠюᆸဋ/% 60 更显著，因此定位性能更好。
Proposed(on-grid)
70
方声源方位角的变化对双耳信号双耳特征的影响
50
40
30 4 结论
针对双耳声源定位中的离格问题，提出了基于
20
-50 0 50 加权宽带稀疏贝叶斯学习的离格双耳声源定位算
வͯᝈ/(O)
(a) ښಫܦູ 法 (WWSBL-OGBSSL)。首先，该算法基于压缩感
知理论建立了离格稀疏双耳信号模型，将离格双耳
90
OC(off-grid)
80 IMF(off-grid) 声源定位问题简化为一个凸优化问题，并采用双耳
வͯᝈͥᝠюᆸဋ/% 60 低噪声和混响的影响，然后通过加权宽带稀疏贝叶
Proposed(off-grid)
相干与扩散能量比特征对各个频点进行加权以降
70
斯学习方法来估计模型参数，最终实现离格声源方
50
位角估计。与现有的离格阵列 DOA 估计算法相比，
40
30 离格双耳声源定位算法既考虑了离格问题的影响，
也考虑了头和躯干的阴影效应的影响。仿真和实际
20
-50 0 50
实验结果表明，本文算法在各种声学环境下都有着
வͯᝈ/(O)
(b) ሏಫܦູ 更高的定位精度和更强的鲁棒性，特别是提高了离
图 5 实际环境下 OC 算法、IMF 算法和 WWSBL- 格条件下的双耳声源方位角估计性能。
OGBSSL 算法的方位角估计准确率
Fig. 5 The azimuth estimation accuracies of the 参 考 文 献
OC, the IMF, the WWSBL-OGBSSL methods in [1] 李军锋, 徐华兴, 夏日升, 等. 基于听觉感知特性的双耳音频
real environments 处理技术 [J]. 应用声学, 2018, 37(5): 706–716.