Page 81 - 《应用声学》2019年第6期

第 38 卷 第 6 期 杜娜等： 有黏条件气泡声散射特性和衰减谱数值研究 983

为比较有黏条件与无黏条件下气泡声散射特 频率，ECAH 模型计算得到的气泡共振特征半径最
性，图 4 给出了单气泡消声系数及散射系数随无因 小，Minnaert 经典公式的计算结果最大，本文计算
次尺寸参量 ka 的变化曲线 (均按静压力为 0.1 MPa 值则介于二者之间。
计算)。从图4中可以看出，与有黏条件相比，无黏条
10 7
1 MHz ඡจங࠱വی
件下消声系数表现为共振区更窄同时峰值更大。此 0.5 MHz ECAH
10 6
外，在 ka < 0.1 时 (共振区)，吸收效应占比较强，散 0.1 MHz
射相对较弱，为散射吸收过渡区。而在 ka > 0.1 后， 10 5
消声系数与散射系数曲线几乎重合，吸收效应几乎 α/(Np·m -1 ) 4
可以忽略，ka = 0.1 为区分纯散射区与散射吸收过 10
渡区的分界线。 10 3
10 4
10 2
10 3 1 10 100
a/µm
10 2
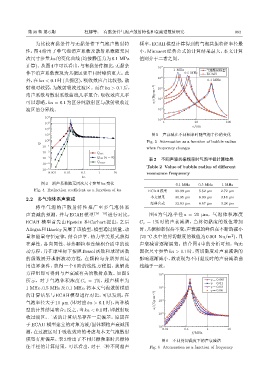
10 1 图 5 声衰减在不同频率时随气泡半径的变化
10 0 Fig. 5 Attenuation as a function of bubble radius
Q
10 -1 when frequency changes
10 -2
Q ext
10 -3 Q ext (η=0) 表 2 不同声波共振频率时气泡半径计算结果
10 -4 Q scatt
Table 2 Value of bubble radius of different
10 -5
0.001 0.01 0.1 1 10 resonance frequency
ka
图 4 消声系数随无因次尺寸参量 ka 变化 0.1 MHz 0.5 MHz 1 MHz
Fig. 4 Extinction coefficient as a function of ka ECAH 模型 29.99 µm 5.52 µm 2.72 µm
2.2 多气泡体系声衰减 本文结果 30.95 µm 6.09 µm 3.18 µm
经典公式 32.83 µm 6.57 µm 3.28 µm
将单气泡的声散射特性推广至多气泡体系
声衰减的预测，并与 ECAH 模型 [16−18] 进行对比。 图 6 为气泡半径 a = 20 µm，气泡体积浓度
ECAH 模型首先由 Epstein 和 Carhart 提出，之后 C v = 1% 时的声衰减谱，当剪切黏度的数值增加
Allegra和Hawley发展了该模型，模型通过质量、动 时，共振频率保持不变，声衰减的峰值在不断的减小
2
量和能量守恒定律，结合声学、热力学关系式获得 (20 ℃ 水中的剪切黏度的数值为 0.001 N·s/m )，且
在弹性、各向同性、导热颗粒和连续相介质中的波 声衰减谱逐渐展宽。结合图 4 中的分析可知，当无
动方程，并在球坐标下按照 Bessel 函数和球谐函数 因次尺寸参量 ka > 0.1 时，剪切黏度对声衰减谱的
的级数展开求解波动方程，在颗粒与介质界面运 影响逐渐减小，故表现为不同黏度时的声衰减谱曲
用边界条件，获得一个 6 阶的线性方程组，求解此 线趋于一致。
方程组即可得到与声衰减有关的散射系数。如图 5 10 6
所示，对于气泡体积浓度 C v = 1%，超声频率为 η=0.001
η=0.01
1 MHz、0.5 MHz 及0.1 MHz，将本文气泡散射模型 10 5 η=0.03
η=0.06
的计算结果与 ECAH 模型进行对比，可以发现，在
气泡半径大于 10 µm (即对应 ka > 0.1 时)，两种模 α/(Np·m -1 ) 10 4
型的计算结果吻合；反之，当ka < 0.1 时，即散射吸
10 3
收过渡区，二者的计算结果存在一定偏差。原因在
于ECAH 模型建立的对象为液/固体颗粒声衰减预
10 2
0.01 0.1 1 10
测，在过渡区对于吸收效应的考虑与本文气泡散射 f/MHz
模型有所偏差。表 2 给出了不同共振频率时共振特 图 6 不同剪切黏度下的声衰减谱
征半径的计算结果。可以看出，对于三种不同超声 Fig. 6 Attenuation as a function of frequency