Page 82 - 《应用声学》2019年第6期

984 2019 年 11 月

图 7 给出气泡体积浓度 C v = 1%，半径 a 分别 3 结论
为30 µm、50 µm、80 µm的声衰减谱，计算结果在数
值及趋势上与 ECAH 模型保持一致。可以看出，随 本文研究了有黏条件下单气泡的声散射特性
着频率的增大，或随着气泡半径增加，声衰减呈减小 及对多气泡的声衰减进行预测，通过理论模型的建
的趋势(此时为非共振区)。同时，图7中还给出了气 立以及计算，得出以下结论：
泡半径 a = 50 µm、体积浓度 C v = 2% 时的声衰减 (1) 通过对单气泡的声散射特性分析可得随
谱，可以看出，随着体积浓度增加一倍，声衰减呈正 着谐波阶数改变，前向散射增加较为明显且散射
比例增加。 旁瓣数先增加后减小。静压力增加时共振区偏移、

650 声衰减减小；频率较小时，共振区的声衰减增强，
50 µm, C v=2%
600 ඡจங࠱വی
ECAH ka = 0.1成为纯散射区与过渡区的分界线。
550
(2) 在对多气泡体系的声衰减进行预测中，浓
500
30 µm 度一定时，当ka > 0.1时，气泡散射模型的计算结果
α/(Np·m -1 ) 400 50 µm 与 ECAH 模型吻合且剪切黏度影响声衰减谱共振
450
350
300
250 峰的展宽和幅值。在非共振区，声衰减随频率的增
80 µm 加而减小，随体积浓度递增且在本文计算的浓度范
200
150 围内呈线性分布。
100
1 2 3 4 5 6 7 8 本文的理论模型为气泡声衰减及气泡粒度表
f/MHz
征提供理论依据。同时，本文工作有助于后续将对
图 7 声衰减随频率的变化
多气泡的理论模型进行拓展以适用于更为复杂的
Fig. 7 Attenuation as a function of frequency
混合颗粒两相流体系。
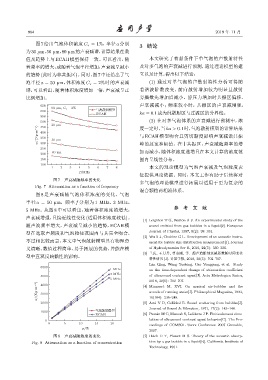
图 8 是声衰减随气泡体积浓度的变化，气泡
半径 a = 50 µm，频率 f 分别为 1 MHz、3 MHz、
参 考 文 献
5 MHz。从图 8 中可以看出，随着体积浓度的增大，
声衰减增强，且接近线性变化(适用体积浓度较低)。
[1] Leighton T G, Walton A J. An experimental study of the
随声波频率增大，声衰减呈减小的趋势，ECAH 模 sound emitted from gas bubbles in a liquid[J]. European
型在选取声频段和气泡粒径范围内与其完全吻合， Journal of Physics, 1987, 8(2): 98–104.
[2] Wu X J, Chahine G L. Development of an acoustic instru-
不过相比较而言，本文中气泡散射模型具有物理意 ment for bubble size distribution measurement[J]. Journal
义清晰、数值过程简单、易于拓展的优势，并能在模 of Hydrodynamics Ser B, 2010, 22(5): 330–336.
[3] 兰庆, 王月兵, 曹永刚, 等. 超声造影剂衰减系数随时间变化
型中直观反映黏性的影响。
特性研究 [J]. 计量学报, 2018, 39(5): 702–707.
Lan Qing, Wang Yuebing, Cao Yonggang, et al. Study
6000
1 MHz on the time-dependent change of attenuation coefficient
3 MHz
5000 of ultrasound contrast agent[J]. Acta Metrologica Sinica,
5 MHz 2018, 39(5): 702–707.
α/(Np·m -1 ) 3000 [4] Minnaert M. XVI. On musical air-bubbles and the
4000
sounds of running water[J]. Philosophical Magazine, 1933,
16(104): 235–248.
2000 [5] Azzi V D, Celikkol B. Sound scattering from bubbles[J].
Journal of Sound & Vibration, 1971, 17(2): 143–148.
1000 ඡจங࠱വی
ECAH [6] Pauzin M C, Mensah S, Lefebvre J P. Finite element simu-
0 lation of ultrasound contrast agent behavior[C]. The Pro-
0 5 10 15 20
ceedings of COMSOL Users Conference 2007 Grenoble,
ϕ/%
2007.
图 8 声衰减随浓度的变化 [7] Hsieh D Y, Plesset M S. Theory of the acoustic absorp-
Fig. 8 Attenuation as a function of concentration tion by a gas bubble in a liquid[R]. California Institute of
Technology, 1961.