Page 26 - 《应用声学》2020年第1期

22 2020 年 1 月

速度频散曲线。可以看到，较低频厚积时，相对于 衰减最大；钢管两侧均为水时，泄漏衰减介于二者
S 0 模式，在一定频厚积范围，A 0 模式相速度与群速 之间。需要注意的是快速水泥情形，由于其纵波声
度的变化较小。对于通常的 8 ∼ 10 mm 厚套管，在 速大于 A 0 模式相速度，故 A 0 模式的泄漏仅向水泥
100 kHz ∼ 400 kHz 频率范围，虽然其相速度有一 辐射横波，因此，其衰减反而小于慢速水泥情形，甚
定变化，但群速度较为平直，近似为“常群速度”。因 至小于两侧液体情形。图3 为频率200 kHz时，理论
此，对该模式波包可以实现较为精确的声时与包络 计算的 A 0 模式泄漏衰减随钢板下侧粘结材料特性
幅度检测，适合于实际工程超声应用。 阻抗的变化曲线。计算时考虑到钢板下侧粘结材料
3
10 密度变化范围相对较小，固定其为 1800 kg/m 。在
9 保持其纵横波速度的比值为1.8708、即泊松比为 0.3
A 
8
固定不变时，改变粘结材料的纵波速度从 1000 m/s
7
ᄱᤴए/(kmSs -1 ) 5 4 S  漏衰减随材料特性阻抗变化的连续曲线。图 3 中分
S 
增加到4500 m/s，步长10 m/s，数值计算A 0 模式泄
6
2 3 A  ืʹᤴए 1250 m/s 别标识了几个典型材料的位置，旨在直观说明气体、
液体 (水)及典型的水泥在特性阻抗-A 0 模衰减坐标
ืʹᤴए 1500 m/s
1
ืʹᤴए 1750 m/s 平面上是明显分离的。因此通过分别测量套管井管
0
0 1 2 3 4 5 6
外材料特性阻抗与沿管壁传播的A 0 模衰减，可以有
ᮠԒሥ/(MHzSmm)
(a) ᄱᤴए 效分类管外材料。
6
3.5
5 S  S  3.0
Ꮖᤴए/(kmSs -1 ) 4 3 A  A  ᄱᤴए/(kmSs -1 ) 2.5

2.0
1.5
2
ืʹᤴए 1250 m/s 1.0 FSV(ቇඡ)
1 ืʹᤴए 1500 m/s FSF(ඵ)
FSS(ਥᤴඵซ)
ืʹᤴए 1750 m/s 0.5 FSS(ঌᤴඵซ)
0
0 1 2 3 4 5 6 0
0 0.2 0.4 0.6 0.8 1.0
ᮠԒሥ/(MHzSmm)
ᮠဋ/MHz
(b) Ꮖᤴए
(a) A 0 വरᄱᤴएజጳ
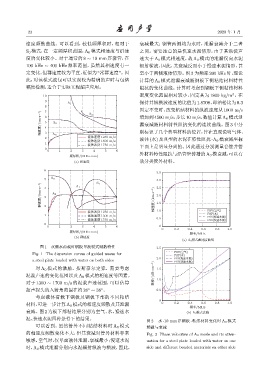
图 1 双侧水荷载时钢板导波模式频散特性 2.5
Fig. 1 The dispersion curves of guided waves for FSV(ቇඡ)
FSF(ඵ)
2.0 FSS(ਥᤴඵซ)
a steel plate loaded with water on both sides FSS(ঌᤴඵซ)
对 A 0 模式的激励，按斯奈尔定律，需要考虑 1.5
泥浆声速的变化范围以及A 0 模式的相速度等因素。 ᛰѓ/(dBScm -1 )
对于 1300 ∼ 1700 m/s 的泥浆声速范围，可以估算 1.0
超声探头的入射角范围在约28 ∼ 38 。 0.5
◦
◦
考虑液体荷载下钢板及钢板下部的不同粘结
0
材料，可进一步计算A 0 模式的相速度频散及其泄漏 0 0.2 0.4 0.6 0.8 1.0
ᮠဋ/MHz
衰减。图 2 为板下部粘结层分别为空气、水、慢速水 (b) A 0 വरᛰѓ
泥、快速水泥四种条件下的结果。 图 2 水 -10 mm 厚钢板 -粘结材料变化时 A 0 模式
可以看到，虽然管外不同粘结材料时 A 0 模式 频散与衰减
的相速度频散变化不大，但其衰减对管外材料非常 Fig. 2 Phase velocities of A 0 mode and its atten-
敏感。空气时，仅单面液体泄漏，衰减最小；慢速水泥 uation for a steel plate loaded with water on one
时，A 0 模式泄漏分别向水泥辐射纵波与横波，因此， side and different bonded materials on other side