Page 21 - 《应用声学》2020年第1期

第 39 卷 第 1 期 郭俊鑫等： 含平行裂缝储层中地震波频散、衰减及频变各向异性 17

介质与裂缝中均填充有水，其体积模量为2.25 GPa， 分析结果，同时给出了仅考虑散射效应的结果及基
3
黏度为 0.001 Pa·s，密度为 1.09 g/cm ，样品几何形 于 Biot 孔弹性理论的数值模拟结果。由图 10 可看
态如图9所示。 出，由于流体运动与散射机制的耦合，随着频率的增
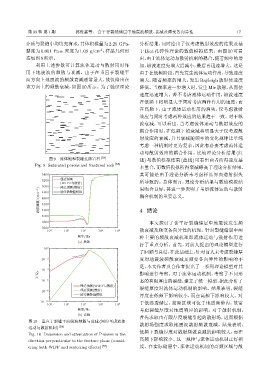
利用上述参数可计算流体运动与散射同时作 加，纵波速度先增大后减小，最后再迅速增大。这是
用下地震波的频散与衰减。由于在垂直于裂缝平 由于在低频阶段，首先发生流体运动作用，导致速度
面方向上地震波的频散衰减通常最大，故仅给出在 增大，随着频率的增大，发生 Rayleigh 散射使速度
该方向上的频散衰减，如图 10 所示。为了验证理论 降低。当频率进一步增大时，发生 Mie散射，从而使

速度迅速增大。若不考虑流体运动作用，纵波速度
在低频下将明显大于同时考虑两种作用的速度，而
在高频下，由于流体运动作用的消失，仅考虑散射
效应与同时考虑两种效应的结果趋于一致。对于纵
波衰减，可以看出，当考虑流体运动与散射效应的
耦合作用时，在低频下的衰减将明显大于仅考虑散
射效应的衰减，并且衰减随频率的变化规律比单纯
考虑一种机制时更为复杂，因此有必要考虑流体运
动与散射效应的耦合作用。比较理论分析结果 (红
图 9 流体饱和裂缝孔隙岩石 [58] 线) 与数值模拟结果 (蓝线) 可看出两者所得速度基
Fig. 9 Saturated porous and fractured rock [58]
本重合，而数值模拟所得衰减略高于理论分析结果，
5400 其可能是由于理论分析未考虑样品界面透射损失
5200 ေ᝷ᮕ฾ 所导致的。总体而言，理论分析结果与数值模拟结
(WIFFˁங࠱)
5000 ေ᝷ᮕ฾(ங࠱) 果吻合良好，其进一步表明了考察流体运动与散射
ጫฉᤴए/(mSs -1 ) 4600 耦合机制的重要意义。
ฉ͜୧஝ϙവલ
4800
4400
4200
4000 4 结论
3800 本文探讨了含平行裂缝储层中地震波发生频
3600
10 0 10 2 10 4 10 6 10 8 散衰减及频变各向异性的机理。针对裂缝储层中两
ᮠဋ/Hz 种主要的频散衰减机理即流体运动与散射作用进
(a) ᮠங
行了重点分析。首先，对前人提出的理论模型进行
10 0
了回顾与总结，在此基础上，针对前人未考虑裂缝厚
10 -2 度对地震波频散衰减及频变各向异性的影响的不
足，本文作者及合作者提出了一系列理论模型对其
10 -4
⊳Q p 影响进行考察。对于流体运动机制，考察了不同形
10 -6 态的有限厚度的裂缝，建立了统一模型，据此分析了
ေ᝷ᮕ฾(WIFFˁங࠱) 裂缝厚度对流体运动机制的影响。结果表明，裂缝
10 -8 ေ᝷ᮕ฾(ங࠱)
ฉ͜୧஝ϙവલ 厚度在低频下影响较小，而在高频下影响较大。对
10 -10 于低渗透储层，高频区域可位于地震频带内，故需
10 0 10 2 10 4 10 6 10 8
ᮠဋ/Hz 考虑裂缝厚度对地震响应的影响。对于散射机制，
(b) ᛰѓ
首先求取由有限厚度裂缝引起的散射场，进而根据
图 10 垂直于裂缝平面纵波频散与衰减 (同时考虑流体
散射场强度求取地震波散射频散衰减。结果表明，
运动与散射机制) [58]
低频下裂缝厚度对散射频散衰减的影响较大，而在
Fig. 10 Dispersion and attenuation of P-waves in the
direction perpendicular to the fracture plane (consid- 高频下影响较小。这一规律与流体运动机制正好相
ering both WIFF and scattering effects) [58] 反。在实际储层中，流体运动机制的高频区域与散