Page 20 - 《应用声学》2020年第1期

16 2020 年 1 月

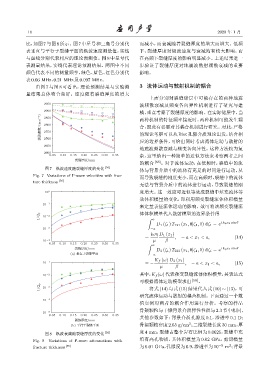
比，如图 7 与图 8 所示。图7 中星号和三角号分别代 而减小，而衰减随着裂缝厚度的增大而增大。低频
表垂直与平行于裂缝平面的纵波速度测量值，实线 下，裂缝厚度对纵波速度与衰减均有较大影响，而
与虚线分别代表相应的理论预测值。图 8 中星号代 在高频下裂缝厚度的影响明显减小。上述结果进一
表测量结果，实线代表理论预测结果。两图中不同 步验证了裂缝厚度对地震波散射频散衰减的重要
颜色代表不同的测量频率，绿色、蓝色、红色分别代 影响。
表0.66 MHz、0.21 MHz及0.097 MHz。
由图 7 与图 8 可看出，理论预测结果与实验测 3 流体运动与散射机制的耦合
量结果总体吻合良好。速度随着裂缝厚度的增大
上面分别对裂缝储层中可能存在的两种地震
2950
波频散衰减及频变各向异性机制进行了研究与建
2900
模，重点考察了裂缝厚度的影响。在实际储层中，当
ጫฉᤴए/(mSs -1 ) 2800 合，因此有必要对其耦合机制进行研究。对此，严格
2850
两种机制的特征频率接近时，两种机制可能发生耦
2750
的理论考察可以从 Biot 孔隙介质理论出发，结合相
2700
应的边界条件，可给出同时考虑流体运动与散射的
2650
地震波频散衰减与频变各向异性。这种方法较为复
2600
0.05 0.10 0.15 0.20 0.25 0.30 0.35 杂，这里给出一种简单的近似方法来考察两者之间
ᜈᎋԒए/mm
的耦合 [58] 。对于流体运动，在低频时，裂缝中的流
图 7 纵波速度随裂缝厚度的变化 [56]
体与背景介质中的流体有充足的时间进行运动，从
Fig. 7 Variations of P-wave velocities with frac-
而导致裂缝的刚度变小，而在高频时，裂缝中的流体
ture thickness [56]
无法与背景介质中的流体进行运动，导致裂缝的刚
10 0 度增大。这一效应可近似等效成裂缝中填充流体等
效体积模量的变化，即利用频变裂缝流体体积模量
10 -1
来定量表征流体运动的影响。故可将该频变裂缝流
1/Q p 10 -2 体体积模量代入散射模型的边界条件得
a
∫
D 1 (ζ 1 ) T 121 (x 1 , 0|ζ 1 , 0) dζ 1 − e ik p x 1 sin θ
10 -3 −a
iωη D 1 (x 1 )
= , − a < x 1 < a, (14)
10 -4 µ β
0.05 0.10 0.15 0.20 0.25 0.30 0.35
a
∫
ᜈᎋԒए/mm D 2 (ζ 1 ) T 222 (x 1 , 0|ζ 1 , 0) dζ 1 − e ik p x 1 sin θ
(a) ۇᄰ̆ᜈᎋࣱ᭧ −a
K f (ω) D 2 (x 1 )
10 -1 = − , − a < x 1 < a, (15)
µ β
10 -2 其中，K f (ω)代表频变裂缝流体体积模量，其表达式
可根据流体运动模型求出 [58] 。
1/Q p 10 -3 将式 (14) 与式 (15) 结果代入式 (10) ∼ (13)，可

研究流体运动与散射的耦合机制。下面通过一个数
10 -4
值实例对两者的耦合作用进行分析。考察的样品
骨架颗粒与干燥背景介质弹性性质与 2.3节中相同，
10 -5
0.05 0.10 0.15 0.20 0.25 0.30 0.35
其他参数如下：背景介质孔隙度 0.1，渗透率 0.1 D；
ᜈᎋԒए/mm
3
(b) ࣱᛡ̆ᜈᎋࣱ᭧ 骨架颗粒密度2.65 g/cm ；二维裂缝长度30 mm，厚
图 8 纵波衰减随裂缝厚度的变化 [56] 度 4 mm，裂缝占整个岩石比例为 0.0625，裂缝中充
Fig. 8 Variations of P-wave attenuations with 填有高孔物质，其体积模量为 0.02 GPa，剪切模量
2
fracture thickness [56] 为0.01 GPa，孔隙度为0.9，渗透率为10 −9 m ；背景