Page 19 - 《应用声学》2020年第1期

第 39 卷 第 1 期 郭俊鑫等： 含平行裂缝储层中地震波频散、衰减及频变各向异性 15

其中，左侧代表背景介质一侧切向与法向应力，右侧 减小，在高频下，裂缝厚度的影响可忽略不计。需要
代表裂缝一侧的相应值；D 1 与 D 2 分别代表裂缝表 注意的是，不同于流体运动，这里低频指的是入射纵
面的切向与法向位移；T 121 (·) 与 T 222 (·) 代表核函 波的波长大于裂缝尺寸的情况，对于该组参数，裂缝
数；µ 代表背景介质剪切模量；η 与 K f 分别代表裂 厚度的影响在地震频带内最大。因此，对于分布有
缝中流体黏度与体积模量；β 代表裂缝厚度。 大尺度裂缝的储层，如碳酸盐岩储层，地震勘探中需
利用数值方法可求解式 (8) 与式 (9) 获得裂缝 要考虑裂缝厚度对地震波散射频散衰减的影响。反
表面的切向与法向位移，进而可求得散射位移场强 过来，根据裂缝厚度与地震波散射频散衰减的关系，
度如下： 可以开发相应的地震属性对裂缝厚度进行探测。
a
∫
ϕ j (k p , θ) = D j (ζ 1 ) e −ik p ζ 1 sin θ dζ 1 , 6300
−a
j = 1, 2. (10) 6250
ጫฉᤴए/(mSs -1 ) 6150
通过散射位移场强度即可求取散射因子，并进 6200
而获得纵波的散射频散与衰减：

k p 6100 β → 0 m
β=0.2 m
κ = vϕ 1 γk p sin 2θ sin θ + vϕ 2
2γ cos θ 6050 β=0.3 m
β=0.4 m
( 2 ) 2
× 1 − 2γ sin θ , (11) 6000
10 1 10 2 10 3
V pe cos θ ᮠဋ/Hz
= 1 − Reκ, (12)
V p k p (a) ᮠங
cos θ 10 -1
−1
Q = 2 Imκ, (13)
p
k p
2
2
其中，γ = V /V ，V s 与 V p 分别为背景介质中的横 10 -2
p
s
波与纵波速度；ν 为单位面积内裂缝的数量；V pe 与 1/Q p
Q −1 为纵波在不同频率下的速度与衰减。 β → 0 m
p
10 -3 β=0.2 m
具体模型推导过程可参见文献[56]。
β=0.3 m
β=0.4 m
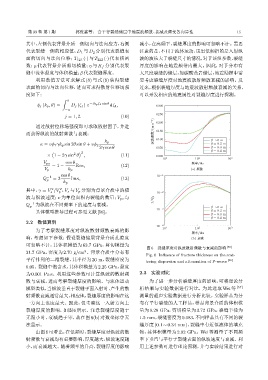
2.2 数值算例
10 -4 1 2 3
为了考察裂缝厚度对纵波散射频散衰减的影 10 10 10
ᮠဋ/Hz
响，考虑如下参数：假设裂缝储层背景介质孔隙度 (b) ᛰѓ
可忽略不计，其体积模量为 63.7 GPa，剪切模量为
图 6 裂缝厚度对纵波散射频散与衰减的影响 [56]
3
31.7 GPa，密度为 2.70 g/cm 。背景介质中分布有
Fig. 6 Influence of fracture thickness on the scat-
平行排列的二维裂缝，其半径为 20 m，裂缝密度为 [56]
tering dispersion and attenuation of P-waves
0.05。裂缝中饱含水，其体积模量为2.25 GPa，黏度
为 0.001 Pa·s。利用这些参数可计算纵波的散射频 2.3 实验对比
散与衰减，进而考察裂缝厚度的影响。与流体运动 为了进一步分析裂缝厚度的影响，可将理论分
模型类似，当纵波垂直于裂缝平面入射时，产生的散 析结果与实验数据进行对比，为此选取 Wei 等 [57]
射频散衰减通常最大，相应地，裂缝厚度的影响在这 测量的超声实验数据进行分析比较。实验样品为分
一方向上也应最大。因此，仅考察这一入射方向上 布有平行裂缝的人工样品，样品背景介质的体积模
裂缝厚度的影响，如图 6 所示。注意裂缝厚度趋于 量为 9.28 GPa，剪切模量为 3.72 GPa，裂缝半径为
无限小时，衰减趋于零，故在图 6(b) 对数坐标中无 1.5 mm，裂缝密度为 0.083，不同样品具有不同的裂
法显示。 缝厚度 (0.1 ∼ 0.34 mm)，裂缝中有近似流体的填充
由图 6可看出，在低频时，裂缝厚度对纵波的散 物，其体积模量为 2.02 GPa。Wei 等测量了不同频
射频散与衰减均有重要影响，厚度越大，纵波速度越 率下垂直与平行于裂缝表面的纵波速度与衰减。利
小，而衰减越大。随着频率的升高，裂缝厚度的影响 用上述参数可进行理论预测，并与实验结果进行对