Page 36 - 《应用声学》2020年第1期

32 2020 年 1 月

以图 3 为例，前两项和前三项之和见图 4，从 然后把鬼波从记录中减掉，这样可以完全恢复一次
图 4 可以看出，随着式 (5) 每一项的加入，鬼波和一 波的信号。
次波分得越来越开，当加到无穷多项时，一次波和鬼
波距离无限远，通过截取序列前面部分数据，把鬼波 2 数值算例
丢掉，可以得到只含一次波的数据。
为了进一步验证本文方法的正确性，首先设
1.0 计了一个简单的层状介质模型 (图 6)，网格间距为
0.5 6.25 m×6.25 m，震源子波是主频 50 Hz 的高斯子
ࣨए 0 波，缆深 25 m，缆长 4000 m，最小偏移距 200 m，
-0.5 震源位置 (x, z) 为 (50 m, 6.25 m)，时间采样步长
-1.0 0.25 ms，记录长度3.5 s。
-1.5
0 0.2 0.4 0.6 0.8 1.0 0 3000
௑ᫎ/s
(a) Ғːᮊ֗ 500
2500
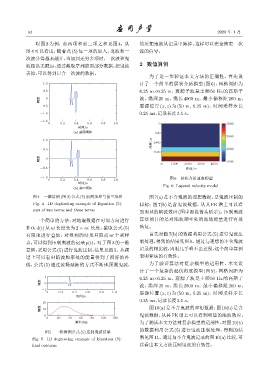
ງए/m 1000
1.0
0.5 2000
1500
ࣨए 0 1500
0 1000 2000 3000 4000
-0.5 ᡰሏ/m

-1.0 层状介质速度模型
0 0.2 0.4 0.6 0.8 1.0 图 6
௑ᫎ/s
Fig. 6 Layered velocity model
(b) Ғʼᮊ֗
图 4 一维算例 (图 3) 公式 (5) 前两项和与前三项和 图 7(a) 是不含鬼波的理想数据，是鬼波压制的
Fig. 4 1D deghosting example of Equation (5): 目标；图 7(b) 是含鬼波数据，从其 FK 谱上可以看
sum of two terms and three terms
到明显的陷波效应 (图中黑色箭头所示)。压制鬼波
一个简单的方法：对地震数据在时间方向进行 算法的目的是对陷波频率处的波场能量进行有效
补 0，d(t) 从 nt 长度变为 2 × nt 长度，截取公式 (5) 恢复。
有限项进行叠加，对得到的结果只取前 nt 个采样 首先对图 7(b) 的数据利用公式 (5) 进行鬼波压
点，可以得到压制鬼波的记录p(t)。对于图3的一维 制处理，得到的结果见图8。通过与理想的不含鬼波
算例，采用公式(5)进行鬼波压制，结果见图5。从频 记录的相比较，肉眼几乎看不出差别，这个简单算例

谱上可以看出陷波频率处的能量得到了很好的补 表明算法的有效性。
偿，公式 (5) 通过波场延拓的方式不断地预测鬼波， 为了验证算法对复杂模型的适用性，本文设
计了一个复杂的起伏海底模型 (图 9)，网格间距为
1 6.25 m×6.25 m，震源子波是主频 50 Hz 的高斯子
ࣨए 0 波，缆深 25 m，缆长 2500 m，最小偏移距 200 m，

-1
0 0.2 0.4 0.6 0.8 1.0 震源位置 (x, z) 为 (50 m, 6.25 m)，时间采样步长
௑ᫎ/s
0.25 ms，记录长度3.5 s。
20
ࣨए 10 图10(a) 是不含鬼波的理想数据；图10(b)是含
0 鬼波数据，从其 FK 谱上可以看到明显的陷波效应。
0 20 40 60 80 100 120
ᮠဋ/Hz 为了测试本文方法对复杂模型的适用性，对图10(b)
的数据利用公式 (5) 进行鬼波压制处理，得到的结
图 5 一维算例公式 (5) 压制鬼波结果
Fig. 5 1D deghosting example of Equation (5): 果见图11。通过与不含鬼波记录的图10(a)比较，可
final outcome 以看出本文方法压制鬼波的有效性。