Page 113 - 《应用声学》2020年第2期

第 39 卷 第 2 期 王文龙等： 基于球形压电陶瓷的耐压水听器 271

壳，并使用 3 个平面对称约束来实现完整球壳。在 振频率变为72.1 kHz，较公式(3)的计算结果稍微增
球面坐标中创建压电材料径向极化坐标系，并使用 大，但并不影响该公式在工程应用上的有效性。由
压电材料 P-51 的材料参数。设定边界载荷为外表 于无法获取该压电材料的相关阻尼系数，因此将模
面受到 0.1 MPa 压力，内表面不受压力。通过执行 型中的柔度矩阵损耗因子和压电矩阵损耗因子设
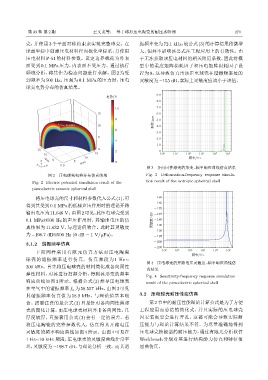
频域分析，将其作为稳态问题进行求解。图 2 为受 置为 0，这导致仿真出该压电球壳在谐振频率处的
到频率为 500 Hz、压强为 0.1 MPa 的压力时，压电 灵敏度为−155 dB，实际上灵敏度应该小于该值。
球壳电势分布的仿真结果。
9.0
ႃҹ/V
8.0
10 7.0
15 6.0
ॎԫ/mm
8 5.0
10 4.0
6
3.0
5 2.0
4
1.0
15 0 2 0
10 15 10 0 10 1 10 2 10 3 10 4 10 5
10 ᮠဋ/Hz
x mm 5 5 0
z y 0 0 mm
图 3 各向同性球壳的形变 -频率响应曲线仿真结果
图 2 压电球壳电势分布仿真结果 Fig. 3 Deformation-frequency response simula-
Fig. 2 Electric potential simulation result of the tion result of the isotropic spherical shell
piezoelectric ceramic spherical shell
将压电球壳的尺寸和材料参数代入公式(1)，可 -160
-165
得到其受到0.1 MPa的低频声压作用时的理论开路
-170
输出电压为11.646 V。由图2可见，此压电球壳受到 -175
0.1 MPa@500 Hz 的声压作用时，其输出电压的仿 ༧ஐए/dB -180
真结果为 11.632 V，与理论值吻合。此时其灵敏度 -185
-190
为−198.7 dB@500 Hz (0 dB = 1 V/µPa)。 -195
-200
3.1.2 谐振频率仿真
-205
下面同样采用有限元仿真方法对压电陶瓷 10 0 10 1 10 2 10 3 10 4 10 5
ᮠဋ/Hz
球壳的谐振频率进行仿真，仿真频段为 1 Hz ∼
图 4 压电球壳的开路电压灵敏度 -频率响应曲线仿
200 kHz。首先将压电球壳的材料简化成各向同性
真结果
弹性材料，对其进行扫频分析，得到其形变的频率
Fig. 4 Sensitivity-frequency response simulation
响应曲线如图 3 所示。根据公式 (3) 推导压电球壳 result of the piezoelectric spherical shell
在空气中的谐振频率 f a 为 58.557 kHz，由图 3 可见
其谐振频率仿真值为 58.9 kHz，与理论值基本吻 3.2 压电球壳耐压性能仿真
合。需要注意的是公式 (3) 只是针对各向同性薄球 第2节中的耐压性能理论计算公式是为了方便
壳的简化计算，而压电球壳材料并非各向同性，且 工程应用而总结的简化式，并且实际的压电球壳
厚度较厚，直接套用公式 (3) 会有一定的误差。若 因安装需要会进行开孔，这都可能会导致实际耐
将压电陶瓷的完整参数代入，仿真得其开路电压 压能力与理论计算结果不符。为尽量准确地得到
灵敏度的频率响应曲线如图 4 所示。由图 4 可见在 压电球壳换能器的耐压能力，通过有限元分析软件
1 Hz∼10 kHz 频段，压电球壳的灵敏度曲线非常平 Workbench 分别对其进行结构静力仿真和特征值
坦，灵敏度为 −198.7 dB，与理论分析一致。而其谐 屈曲仿真。