Page 93 - 《应用声学》2020年第2期

第 39 卷 第 2 期 叶瑾等： 一种改进的时变转移概率 AIMM 跟踪算法 251

1.0 0.8
CVവی
0.7
0.8 ࢻᣁिCTവی
0.6 ԿᣁिCTവی
CVവی
വیഐဋ 0.4 ࢻᣁिCTവی വیഐဋ 0.5
0.6
0.4
0.2 ԿᣁिCTവی 0.3
0.2
0 0.1
0 50 100 150 200 250 300 350 0 50 100 150 200 250 300 350
᧔ನ௑҉/s ᧔ನ௑҉/s
(a) వ஡AIMMካขՊവیഐဋ (b) ͜ፒIMMካขՊവیഐဋ
1.0 1.0
CVവی
0.8 ࢻᣁिCTവی 0.8
ԿᣁिCTവی CVവی
വیഐဋ 0.4 വیഐဋ 0.6 ԿᣁिCTവی
ࢻᣁिCTവی
0.6
0.4
0.2 0.2
0 0
0 50 100 150 200 250 300 350 0 50 100 150 200 250 300 350
᧔ನ௑҉/s ᧔ನ௑҉/s
(c) ஡࿹[6]ካขՊവیഐဋ (d) ஡࿹[8]ካขՊവیഐဋ

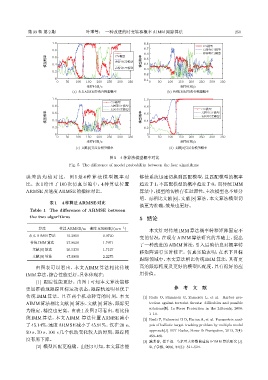
图 5 4 种算法模型概率对比
Fig. 5 The difference of model probability between the four algorithms

误 差 的 均 值 对 比， 图 5 是 4 种 算 法 模 型 概 率 对 够使系统迅速切换到匹配模型，且匹配模型的概率
比。表 1 给出了 100 次仿真实验中，4 种算法位置 趋近于1，不匹配模型的概率趋近于0。而传统IMM
ARMSE及速度ARMSE的指标对比。 算法中，模型的切换存在迟滞性，主次模型也不够分
明。而相比文献 [6]、文献 [8] 算法，本文算法模型切
表 1 4 种算法 ARMSE 对比
换更为准确，效果也更好。
Table 1 The difference of ARMSE between
the two algorithms 5 结论

算法 位置 ARMSE/m 速度 ARMSE/(m·s −1 )
本文针对传统 IMM 算法概率转移矩阵固定不
本文 AIMM 算法 15.2851 0.9720
变的情况，在现有 AIMM 算法研究的基础上，提出
传统 IMM 算法 27.8626 1.7971
了一种改进的 AIMM算法，引入后验信息对概率转
文献 [6] 算法 26.5270 1.7127
移矩阵进行实时修正。仿真实验表明，在水下目标
文献 [8] 算法 47.8908 2.2275
跟踪领域中，本文算法相比传统 IMM 算法，具有更
由图表可以看出，本文 AIMM 算法相比传统 高的跟踪精度及更好的模型匹配度，具有很好的应
IMM算法，综合性能更好，具体体现在： 用价值。
(1) 跟踪性能更好。由图 1 可知本文算法能够
更加准确地跟踪目标运动状态，跟踪轨迹明显优于 参 考 文 献
传统 IMM 算法。且在两个机动转弯的时刻，本文 [1] Radu O, Slamnoiu G, Zarnescu L, et al. Harbor pro-
AIMM算法相比文献[6] 算法、文献[8] 算法，跟踪更 tection against terrorist threats: difficulties and possible
solutions[R]. In Force Protection in the Littorals, 2006:
为稳定，精度也更高。由表 1 及图 2 可看出，相比传
1–10.
统 IMM 算法，本文 AIMM 算法位置 ARMSE 减小 [2] Reali F, Palmerini G B, Farina A, et al. Parametric anal-
了45.14%，速度ARMSE减小了45.91%。仅在20 s、 ysis of ballistic target-tracking problem by multiple model
50 s、70 s、100 s 几个机动变化较大的时刻，跟踪精 approach[J]. IET Radar, Sonar & Navigation, 2013, 7(4):
459–469.
度有所下降。
[3] 臧荣春, 崔平远. 马尔可夫参数自适应 IFIMM 算法研究 [J].
(2) 模型匹配更准确。由图 3 可知，本文算法能 电子学报, 2006, 34(3): 521–524.