Page 51 - 《应用声学》2020年第6期

第 39 卷 第 6 期 于梦枭等： 浅海单矢量传感器宽带声源三维定位仿真 845

率，当声源频率较大时，声场中的简正模阶数较多， 图 6 为代价函数分布，搜索范围 10∼30 km，带
不同阶简正模的声压与垂直振速之间的相干项特 宽选择 0.2 Hz。红线表示代价函数最大值对应的
征频率差异可能会很小，容易出现混叠，不利于代价 估计距离，初始距离估计值为 15.2 km，相对误差
函数的使用。且随着距离的增加，高阶简正模衰减 1.3 %，继而根据相对速度可以确定其他位置的声源
较大，归一化能量峰值位置可能会发生改变，如图 5 距离。代价函数有一定的主瓣宽度，可能带来估计
所示。为避免该情况的发生，本节仿真声场中仅存 误差，但在可接受的误差范围内。
在三阶简正模。 不改变仿真条件，在原信号中加入高斯白噪声，
分析不同信噪比条件下测距方法的相对误差。图 7
25
为不同的信噪比条件下，测距结果的相对误差情况
(图中纵轴截取至30%)。当信噪比大于10 dB时，估
ܦູᡰሏ/km 20 计结果相对误差小于 11.33%，在未进行任何信号时

间累积预处理时，该测距方法的实现需要较高的信
噪比。
150
15
5 10 15 20 25 30
ᮠဋ/Hz
(a) ϜࠀѺݽᡰሏ˞15 km 100
F↼r↽
45
50
ܦູᡰሏ/km 40 0 10 15 20 25 30

ᡰሏ/km

图 6 信号初始距离为 15 km 的代价函数
35
5 10 15 20 25 30 Fig. 6 Cost-function at the initial range of 15 km
ᮠဋ/Hz
(b) ϜࠀѺݽᡰሏ˞35 km 30
图 4 假定不同的初始距离，仅有前三阶简正模时的 25
F T W T (r, θ, f) 图 20
ᄱࠫឨࣀ/% 15
Fig. 4 Diagram of F T W T (r, θ, f) with first three
order normal modes at different initial range

50 10
5
45
0
10
40 5 η٪උ/dB 15
༠Ⓚ䐍⿫/km 35 图 7 测距估计相对误差随信噪比的变化情况
30
25 Fig. 7 The relative error of range estimation ver-
sus signal-to-noise ratio
20
15 3.3 声源深度估计
5 10 15 20 25 30 35 40
仁⦷/Hz 仿真条件同上，声源距离为 5 km，声源深度范

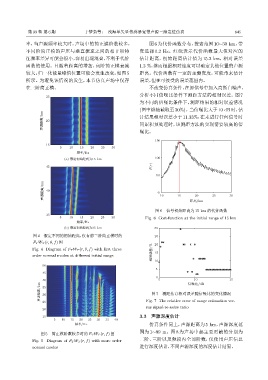
图 5 简正模阶数较多时的 F T W T (r, f) 图 围为 1∼99 m。图 8 为声场中起主要贡献的分别为
Fig. 5 Diagram of F T W T (r, f) with more order 二阶、三阶以及频段内全部阶数，仅使用声压信息
normal modes 进行深度估计，不同声源深度的深度估计结果。