Page 50 - 《应用声学》2020年第6期

844 2020 年 11 月

向匀速运动处理。选择声源频率为50 Hz、声源深度 表 1 波数谱中三阶简正模各物理量的数据统计
为 30 m 的单频点信号进行处理。在工作频段内可 Table 1 Data statistics of each physical
选择任意频率的单频点信号，频率对方法性能无影 quantity of third order normal modes in
响。在频率较低时，多普勒频移导致的影响较小，在 wavenumber spectrum
此忽略其影响。选择声源距离为5∼10 km的信号进 简正模 声压 水平振速 假定水平 水平波数
行处理。假设声源相对径向速度为5 m/s，对声压及 编号 m 峰值 p m 峰值 v rm 波数 k rm假定 理论值 k rm
水平振速进行 Hankel 变换，图 2 为声压及水平振速 1 9.852 9.13 0.385 0.194
的波数谱。 2 14.55 14.21 0.4045 0.205
3 7.235 7.211 0.4155 0.209
15
30

10 25
ࣨϙ 20
5 ᄱࠫឨࣀ/% 15
10

0 5
0.38 0.4 0.42
ඵࣱฉ஝ 0
-10 -5 0 5 10
(a) ܦԍฉ஝៨
η٪උ/dB
15
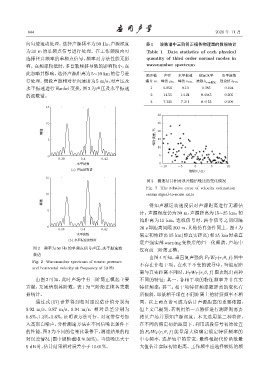
图 3 测速估计相对误差随信噪比的变化情况
Fig. 3 The relative error of velocity estimation
10 versus signal-to-noise ratio
ࣨϙ 得知声源运动速度后对声源距离进行无源估

5
计。声源深度仍为 30 m，声源距离为15∼25 km，初
始距离为 15 km，选取信号时，两个信号之间间隔
0 20 s 即距离间隔 200 m，其他仿真条件同上。图4 为
0.38 0.4 0.42
ඵࣱฉ஝ 假定初始距离 15 km(即真实距离) 和 35 km 时垂直
(b) ඵࣱ૝ᤴฉ஝៨
复声强实部 warping 变换后的归一化频谱，声场中
图 2 频率为 50 Hz 的单频点信号声压、水平振速波 仅有前三阶简正模。
数谱
由图 4 可知，垂直复声强的 F T W T (r, θ, f) 图中
Fig. 2 Wavenumber spectrum of source pressure
不存在非相干项。在水平不变的波导中，当假定距
and horizontal velocity at frequency of 50 Hz
离与真实距离不同时，F T W T (r, θ, f) 图表现出两种
由图 2 可知，此时声场中有三阶简正模起主要 不同的特征：其一，各相干项的特征频率并非真实
贡献，无需辨别其阶数。表 1 为三阶简正模各类数 特征频率；其二，相干项特征频率随距离的变化有
据统计。 所倾斜，即某相干项在不同距离上的特征频率不相
通过式 (17) 计算得到相对速度估计值分别为 同。以上两点皆可成为估计声源距离的重要依据，
9.92 m/s、9.87 m/s、9.94 m/s，相对误差分别为 但上文已提到，若利用第一点特征进行测距则需要
0.8%、1.3%、0.6%，证明该方法可行。对宽带信号加 拷贝声场并预知声源深度。本文选用第二种特征，
入高斯白噪声，分析测速方法在不同信噪比条件下 在不同的假定初始距离下，利用该段信号初始位置
的性能，图3为不同的信噪比条件下，测速结果的相 的 F T W T (r, θ, f) 能量最大值确定假定特征频率的
对误差情况 (图中纵轴截取至 30%)。当信噪比大于 中心频率，选择较窄的带宽，最终根据代价函数最
0 dB时，估计结果相对误差小于10.61%。 大值估计实际初始距离。工作频率应选择较低的频