Page 93 - 《应用声学》2020年第6期

第 39 卷 第 6 期 唐军等： 微织构超声振动铣削系统的研究 887

主要有旋转主运动、进给运功以及纵扭复合超声振 由图 2(b) 可知， 立铣刀刀尖的轴向与周向
动3 部分组成，如图 2(a) 所示。通常情况下，进给运 位移为
功速度远小于主运动速度，故沿铣刀的轴向和周向 
 s = v r0 t + δ θ cos ωt,
建立刀尖的切削模型，如图2(b)所示。 (1)
z = −δ z cos(ωt + α).

㓥
・䬓࠰ ੁ
z
ᥟ 立铣刀刀尖的轴向与周向速度为
ࣘ
᯻䖜䘀ࣘ

 v s = v r0 + δ θ ω sin ωt,
O (2)
 v z = −δ z ω sin(ωt + α).
ᢝ䖜ᥟࣘ
x
y
其中，ω 为超声振动角频率；δ z 、δ θ 表示超声在轴向
(a) ቡᨾѨᨾҐവی
和周向的超声振幅；α 为纵向和扭转超声振动的相
z 位差；v r0 表示瞬时切向速度。
v r
对方程式 (2) 进行求解，获得刀具刀尖在的运
θ
δ θ
◦
δ z 动轨迹(设：相位差为90 )，如图3所示。
基于上述分析，在保证刀具分离切削的前提下，
(b) ቡᨾѨևՔѭҐവی 设定切削线速度为 0.28 m/s，而超声纵振振幅和扭
转振幅依据后续第 4.1 节振幅测试结果进行设定，
图 2 超声椭圆振动系统铣削机理模型
分别为 6.7 µm 和 3.1 µm，利用数学仿真软件在空
Fig. 2 Milling mechanism model of ultrasonic el-
liptical vibration system 间范围内绘制加工工件的表面形貌，如图4所示。

᧘ܭѭҐ
1.2 T⊳ Ѭሏག
ᣉՔͯረ z/10 ֓ m -0.6 0 T⊳ T⊳ ഷՔጻ౞ѨЦ ѭѣག ѭКག
0.6

T
-1.2
ҫࢺࢺ͈᛫
᭧ॎ᠂
-1.8
0 2 4 6 8 10 12
ѨЦᣁᝈ θ/rad
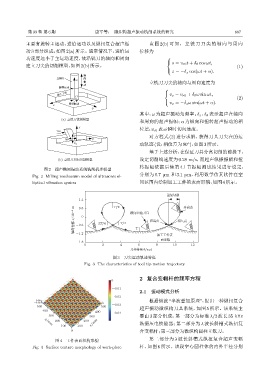
图 3 刀尖运动轨迹特征
Fig. 3 The characteristics of tool tip motion trajectory

2 复合变幅杆的频率方程
0

-0.01
2.1 振动模式分析
-0.02
֓⊲ 根据纵波 “半波叠加原理”，提出一种纵扭复合
֓⊲
-0.03
500 500 超声振动微织构刀具系统，如图 5 所示。该系统主
400 400
-0.04
300 300 要由 3 部分组成：第一部分为标准 λ/2 波长 35 kHz
200 200 x/mm 纵振压电换能器；第二部分为 λ 波长斜槽式纵扭复
y/mm
100 100
0 合变幅杆；第三部分为微织构圆柱立铣刀。
第二部分为 λ 波长斜槽式纵扭复合超声变幅
图 4 工件表面织构形貌
Fig. 4 Surface texture morphology of work-piece 杆，如图 6 所示。该段空心圆柱体的内外半径分别