Page 94 - 《应用声学》2020年第6期

888 2020 年 11 月

2
为R 1 、R 2 ；截面积s = π(R − R )；斜槽相对轴线倾 及连接螺纹与纵扭复合超声变幅杆相连；I-I 面右
2
2
1
角为 θ；A-B 表示纵扭演变的分界线；A-B 左侧空心 侧由圆柱段 L 3 、圆锥段 L 4 以及圆柱段 L 5 三部分组
柱体长度为L 1 ；A-B右侧空心柱体长度为L 2 。 成；L 3 段的半径为 R 3 ，面积 s 3 = πR ；L 4 段锥度
2
3
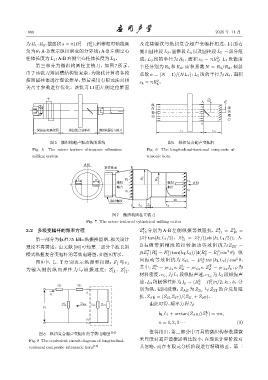
第三部分为微织构圆柱立铣刀，如图 7 所示。 半径分别为 R 3 和 R 4 ，面积系数 N = R 3 /R 4 ，倾斜
由于该铣刀排屑槽结构较复杂，为简化计算将各段 系数 α = (N − 1)/(NL 4 )；L 5 段的半径为 R 4 ，面积
按照圆柱体进行理论推导，然后采用有限元法对相 s 4 = πR 。
2
关尺寸参数进行优化。该铣刀 I-I 面左侧定位锥面 4
R 
A R 
ጫ
Ք ጫ
૝ ੵ
ү ᏹ
Ռ
B
ጫ૝ԍႃ૱ᑟ٨ ጫੵܭՌԫࣨీ ॲጻ౞ړಏቡᨾѨ L  L 2

图 5 微织构超声振动铣削系统 图 6 纵扭复合超声变幅杆
Fig. 5 The micro texture ultrasonic vibration Fig. 6 The longitudinal-torsional composite ul-
milling system trasonic horn
AՔ
ࠀͯ᩼᭧ 

2 2 F 3 R 3 R 4
ጫੵ ጫੵ F 6 AՔ
ᏹՌ ᏹՌ
v 6
v 3
ᤌଌᛃጯ 25
 L 3 L 4 L 5

图 7 微织构圆柱立铣刀
Fig. 7 The micro-textured cylindrical milling cutter
L
L
2.2 多级变幅杆的频率方程 Z 分别为 A-B 左侧纵振等效阻抗，Z L = Z 13 =
11
13
L
L
L
第一部分为标准35 kHz纵振换能器，相关设计 jZ tan(k L L 1 /2)，Z 12 = Z /(j sin(k L L 1 /2))；A-
1
1
理论不再赘述。由文献 [16] 可知第二部分半波长斜 B 右侧带斜槽段的扭转振动等效阻抗为 Z 2T =
2
T
3
3
2
2
槽式纵扭复合变幅杆的等效电路图，如图8所示。 j9Z (R − R ) tan(k T L 2 )/[4(R − R ) sin θ]；纵
1
2
2
1
2
L
2
向振动等效阻抗为 Z 2L = jZ tan(k L L 2 )/ cos θ。
2
图 8 中，L、T 分别表示纵振和扭振；F 1 与 v 1
L L T = ρc L 2 p ，ρ 为
L
L
为输入侧的纵向弹性力与纵振速度；Z 、Z 、 其中，Z = ρc L 1 s，Z = ρc L 2 s，Z 2 I
2
1
12
11
为L 2 段纵振声
材料密度，c L 1 为L 1 段纵振声速，c L 2
速，L 2 段极惯性距为 I p = (R − R )π/2；k L 、k T 分
2
2
L L 2 1
Z 11 Z 13
@ 别为纵、扭圆波数；Z AB 为 Z 2L 与 Z 2T 的合反射阻
A
抗，Z AB = (Z 2L Z 2T )/(Z 2L + Z 2T )。
v 1
L Z AB 由此可得，频率方程为
Z 12 Z 2L Z 2T
F 1
L
k L L 1 + arctan(Z AB /jZ ) = nπ,
1
B
@ n = 1, 2, 3 · · · (3)
值得指出，第三部分中刀具的微织构参数属微
图 8 纵扭复合超声变幅杆的等效电路图 [16]
Fig. 8 The equivalent circuit diagram of longitudinal- 米尺度对超声谐振影响比较小，在理论计算阶段对
torsional composite ultrasonic horn [16] 其忽略，而在有限元分析阶段进行精确修正。第三