Page 106 - 《应用声学》2021年第4期

590 2021 年 7 月

式 (2) 中，u 为 x 方向上的位移分量。忽略散射和衰 那么，材料的二阶非线性系数可表示为
减的影响，一维纵波在固体介质中的波动方程为 8 A 2
β = . (7)
2
2
∂ u ∂σ k x A 2 1
ρ = , (3)
∂t 2 ∂x
根据式 (7)，只需要对实验测量的时域接收
式(3)中，ρ为介质的密度，x为波传播的距离，t为时
信号进行快速傅里叶变换 (Fast Fourier transform,
间。将式 (1)~(2) 带入式 (3) 中，并忽略二阶以上高
FFT) 转换，得到接收信号中基波和二次谐波的幅
阶项可以得到非线性介质中的一维纵波波动方程：
值A 1 和A 2 ，就可以得到材料的二阶非线性系数。实
2
2
2
∂ u ∂ u ∂u ∂ u
ρ = E + 2βE . (4) 验中为了避免超声波近场干涉的影响，选取激励信
∂t 2 ∂x 2 ∂x ∂x 2
当入射波为单频正弦波，即u = A 1 sin (ωt)，其 号经试样下上表面分别反射后的二次波作为接收
中A 1 位基波幅值，ω 为角速度，根据摄动理论，波动 信号。
方程的近似解为
2 有限元模拟方法
u = A 1 sin (kx − ωt)
1 2 2 位错超声非线性理论模型
− βk A x cos 2 (kx − ωt) , (5) 2.1
1
8
式(5)中，k 为波数。根据式(5)，二次谐波幅值A 2 为 金属材料的塑性损伤与位错结构的演化直接
相关。在拉伸载荷作用下，材料内部的位错将发生
1 2 2
A 2 = βk A x. (6)
1
8 增殖、堆积、缠结等变化，并引起超声非线性参数的
改变。位错运动时会被材料内部的杂质原子、第二
1.0
相粒子等钉扎，相邻两钉扎点之间的位错线会在应
力的作用下形成类似弦的弓出。当周期性的应力波
0.5
ॆʷӑࣨϙ 0 作用在位错弦上时，位错弦就会产生受迫振动，使
入射波发生波形畸变，产生高次谐波。晶体中弹性

-0.5 波引起的附加应力 ∆σ 和附加应变 ∆ε 之间的关系
为 [8]
-1.0
2
∂σ 1 ∂ σ 2
0.0 0.2 0.4 0.6 0.8 1.0 ∆σ = (∆ε) + 2 (∆ε) + · · ·
∂ε 2 ∂ε
௑ᫎ/µs
1 2
= A(∆ε) + B(∆ε) + · · · , (8)
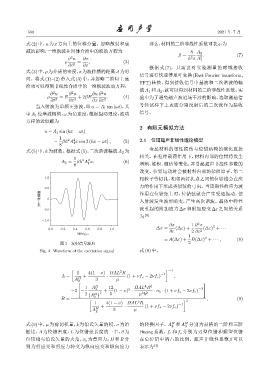
图 3 发射信号波形 2
Fig. 3 Waveform of the excitation signal 式(8)中，

[ 2 ] −1
1 4(1 − ν) ΩΛL R −1
A = H + · (1 + νf s − 2νf e ) ,
A 2 3 µ
[ ]
4
1 A H 12 3 ΩΛL R 3 −3
3
3
−2 − ( ) + (1 − ν) · 3 2 · σ b · (1 + νf s − 2νf e )
2 A H 5 µ b
B = 2 , (9)
[ 2 ] 3
1 4(1 − ν) ΩΛL R −1
+ · (1 + νf s − 2νf e )
A H 3 µ
2
式 (9) 中，µ 为剪切模量，b 为伯氏矢量的模，ν 为泊 的转换因子。A 和 A 分别为晶格的二阶和三阶
H
H
3
2
松比，Λ 为位错密度，L 为位错弦长度的一半，θ 为 Huang 系数，f e 和 f s 分别为刃型位错和螺型位错
位错线与伯氏矢量的夹角，σ b 为背应力，Ω 和 R 分 在总位错中所占的比例。超声非线性系数 β 可以
别为剪应变和剪应力转变为纵向应变和纵向应力 表示为 [4]