Page 108 - 《应用声学》2021年第4期

592 2021 年 7 月

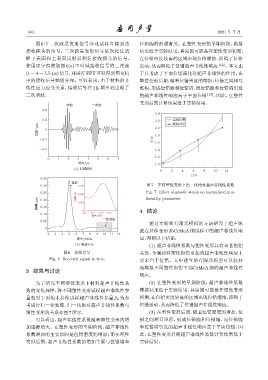
图 6 中一次波是发射信号经过试样直接到达 位错胞的形成有关。在塑性变形的早期阶段，模拟
接收探头的信号，二次波是发射信号依次经过试 结果低于实验结果，其原因可能是在塑性变形初期，
样下表面和上表面反射后到达接收探头的信号。 在位错密度较高的区域出现位错缠结，阻碍了位错
使用汉宁窗截取图 6(a) 中时域接收信号的二次波 运动，从而降低了位错超声非线性响应 [12] 。本文由
(t = 4 ∼ 5.5 µs)信号，并进行 FFT可以得到图 6(b) 于只考虑了平面位错演化对超声非线性的作用，在
中的接收信号频谱分布。可以看出，由于材料的非 塑性变形后期，随着位错密度的增加，位错之间相互
线性应力应变关系，接收信号在 2f 0 频率处出现了 堆积，形成位错胞和位错墙，而位错胞和位错墙引发
二次谐波。 的超声非线性响应高于平面位错 [13] ，因此，在塑性
变形后期计算结果低于实验结果。
ʷ൓ฉ ̄൓ฉ
0.8
2.4
0.4 ࠄᰎፇ౧
2.2 വલፇ౧
ͯረ/µm 0 2.0

β/β 0 1.6
-0.4 1.8
-0.8 1.4
1.2
0 1 2 3 4 5 6 7
௑ᫎ/µs
1.0
(a) ௑۫ฉॎ
0 2 4 6 8 10 12
ε/%
0.35
۳ฉ
0.30 0.012 图 7 不同塑性变形下归一化相对超声非线性系数
0.25 ૝ࣨ/µm 0.008 Fig. 7 Effect of plastic strain on normalized non-
૝ࣨ/µm 0.20 0.004 linearity parameter
0.15
0 4 结论
0.10 9.0 9.5 10.0 10.5
ᮠဋ/MHz
̄൓ៈฉ
0.05
通过实验和有限元模拟的方法研究了超声纵
0
波在拉伸变形 35CrMoA 钢试样中的超声非线性响
2 3 4 5 6 7 8 9 10 11 12
ᮠဋ/MHz 应，得到以下结论：
(b) ᮠ៨Ѭ࣋ (1) 超声非线性系数与塑性变形具有显著的相
图 6 接收信号 关性，金属材料塑性损伤引起的超声非线性响应主
Fig. 6 Received signal in time 要来自于位错。文中建立的有限元模型可以较好

地模拟不同塑性损伤下 35CrMoA 钢的超声非线性
3 结果与讨论
响应。
为了研究不同塑性变形下材料超声非线性系 (2) 在塑性变形的早期阶段，超声非线性系数
数的变化规律，将不同塑性变形试样超声非线性参 模拟结果低于实验结果，其原因可能是在塑性变形
量相对于原始未拉伸试样超声非线性参量 β 0 为参 初期，在位错密度较高的区域出现位错缠结，阻碍了
考进行归一化处理，归一化相对超声非线性系数与 位错运动，从而降低了位错超声非线性响应。
塑性变形的关系如图7所示。 (3) 在塑性变形后期，随着位错密度的增加，位
可以看出，超声非线性系数随着塑性变形的增 错之间相互堆积，形成位错胞和位错墙，而位错胞
加逐渐增大。在塑性变形的早期阶段，超声非线性 和位错墙引发的超声非线性响应高于平面位错，因
系数增加的主要原因是位错密度的增加；而在塑性 此，在塑性变形后期超声非线性系数计算结果低于
变形后期，超声非线性系数的增加主要与位错墙和 实验结果。