Page 43 - 《应用声学》2021年第4期

第 40 卷 第 4 期 罗英勤等： 含周期性空腔结构吸声机理的研究 527

表 1 含空腔结构几何和材料参数
Table 1 The geometry and material param-
eters of the structure containing cavity

一层 二层 钢被衬
杨氏模量 E/MPa 0.001 400 2.1 × 10 5
(a) پ᣸ॎഷ੕᭧ 密度 ρ/(kg·m −3 ) 29 1800 7800
泊松比 v 0.495 0.495 0.3

损耗因子 η 1.6582 1.991 0.001
层厚 t/mm 8.8 1 25

1.0
ᤰߘဋᄱՏᄊړಏʹ
ᤰߘဋᄱՏᄊ̄፥ᣉࠫሦവی
0.8 ቡவʹ
1/4ቡவʹ
(b) О᣸ॎഷ੕᭧ ஡࿹[20]
ծ஝ጇܦ α 0.6
平面周期单元形式
图 1
Fig. 1 Plane periodic unit form 0.4
0.2

0
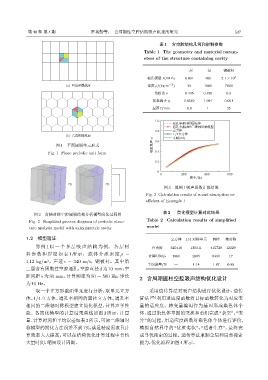
0 200 400 600
ᮠဋ/Hz
图 3 算例 1 吸声系数计算结果
Fig. 3 Calculation results of sound absorption co-
efficient of Example 1

图 2 含轴对称空腔周期结构分析模型简化过程图 表 2 简化模型计算对比结果
Fig. 2 Simplified process diagram of periodic struc- Table 2 Calculation results of simplified
ture analysis model with axisymmetric cavity model

1.2 模型验证 立方体 1/4 对称单元 圆柱 轴对称

算例 1 以一个多层吸声结构为例， 各层材 自由度 326418 130311 415729 12329
料参数和厚度如表 1 所示， 流体介质密度 ρ =
计算时间/s 7860 2885 8390 17
1.12 kg/m³，声速 c = 340 m/s，钢被衬。其中第
平均误差/% — 1.14 1.87 0.88
二层含有周期性空腔通孔，空腔直径d为10 mm，空
腔间距 s 为 30 mm，计算频率为 50 ∼ 500 Hz，步长
2 含周期圆柱空腔吸声结构优化设计
为10 Hz。
取一个正方形截面单元进行分析，取单元立方 采用遗传算法对吸声结构进行优化设计，遗传
体、1/4 立方体、通孔率相同的圆柱立方体、通孔率 算法 [25] 利用适应度函数将目标函数转化为对应变
相同的二维轴对称模型建立简化模型，计算声学性 量的适应度。将变量编码作为基因形成染色体个
能。各简化模型的计算结果曲线如图 3 所示，计算 体，通过染色体基因的变换和重组完成 “杂交”、“变
量、计算时间和平均误差如表2所示，可知二维轴对 异” 的过程，用适应度函数对染色体个体进行评价，
称模型的简化方法误差不到1%，满足精度需求且计 模拟自然界中的 “优胜劣汰”、“适者生存”，最终完
算效率大大提高，可以在结构优化计算过程中节约 成寻优搜索的过程。遗传算法兼顾全局和局部搜索
大量时间，缩短设计周期。 能力，优化流程如图4所示。