Page 34 - 《应用声学》2021年第6期

830 2021 年 11 月

相应地，2016 年测得的数据结果中稳定振荡现象的 底地形平缓。对于坡度足够小的粗糙界面，小斜率
持续时间相对较短，图 3 中 0.14 s 之前可以发现稳 近似在不损失传统近似精度的基础上给出覆盖全
定的振荡现象，在0.14 s 之后，这一稳定的振荡规律 掠射角范围的散射模型，其散射模型对应的散射截
开始消失。从图4可以看出，在0.14 s之前观察到的 面可表示为 [6]
混响强度振荡周期是基本吻合的。两次混响实验的 k |A ww | 2
4
w
σ = I K . (1)
2
测量环境不同，参照文献[2]给出的地形起伏对混响 2π∆K ∆k 2 z
强度衰减趋势的影响，说明本文实验中发现的振荡 对于半无限均匀液态海底模型，
现象不是由海底地形振荡造成的。 1
A ww = [1+V ww (θ i )] [1+V ww (θ s )] G, (2)
2
-30 ( 1 ) ( sin θ pi sin θ ps )
0.5 s G = 1 − cos θ i cos θ s cos ϕ− 2
-40 1.0 s a ρ a a ρ
p
2.0 s 1
-50 4.0 s − 1 + a a ρ , (3)
ຉ־ूए/dB -60 sin θ pi = √ 1−a cos θ i , (4)
2
p
2
2
p
-70
2
2
sin θ ps = √ 1−a cos θ s , (5)
p
-80
∫
∞
( 2α )
I K = J 0 (y)y exp −qy dy, (6)
-90
0 0.1 0.2 0.3 0.4 0.5 0.6 0
௑ᫎ/s πwΓ (2 − α) 2 −2α
2
q = ∆k ∆K −2α , (7)
z
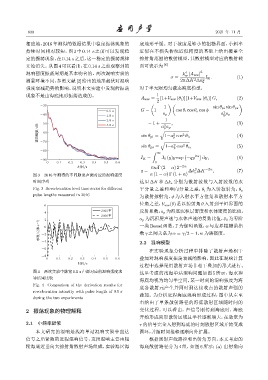
图 3 2016 年测得的不同脉宽声源对应的混响强度 α (1 − α) Γ (1 + α)
时间序列 这里 ∆K 和 ∆k z 分别为散射波数与入射波数的水
Fig. 3 Reverberation level time series for different 平分量之差和垂向分量之差，θ i 为入射掠射角，θ s
pulse lengths measured in 2016
为散射掠射角，ϕ 为入射水平方位角和散射水平方
位角之差，V ww (θ) 是以掠射角 θ 入射到平坦界面的
6
2015ࣲ 反射系数，a ρ 为海底沉积层密度和水体密度的比值，
4
2016ࣲ a p 为沉积层声速与水体声速的复数比值，J 0 为零阶
ර࠮/(dBSs -1 Ď -2 0 一类 Bessel 函数，Γ 为伽玛函数，α 与边界粗糙谱指
2
数γ 之间关系为α = γ/2 − 1，w 为谱强度。
-4 2.2 混响模型
-6
在实验现象分析过程中排除了散射声场相干
-8
0 0.1 0.2 0.3 0.4 0.5 0.6 叠加对混响强度振荡衰减的影响，因此在混响计算
௑ᫎ/s
过程中选择采用散射声场非相干叠加的形式进行。
图 4 两次实验中脉宽 0.5 s 声源对应的混响强度求 这里考虑的浅海单站混响问题如图 5 所示，海水和
导结果比较
海底均视为均匀半空间，某一时刻的混响强度为海
Fig. 4 Comparison of the derivation results for
底各散射元产生并同时到达接收点的散射声强的
reverberation intensity with pulse length of 0.5 s
叠加。为分析近程海底混响形成过程，图中从左至
during the two experiments
右给出了单条散射路径的海底散射区域随时间的
2 振荡现象的物理解释 变化过程，可以看出，声信号刚传到海底时，海底
开始形成圆形散射区域且半径逐渐增大，在脉宽为
2.1 小斜率近似 τ 的信号完全入射到海底的时刻散射区域开始变成
本文研究的混响是浅海单站混响实验中直达 圆环，并随时间推移逐渐向外扩展。
信号之后紧随的近程混响信号，这段混响主要由粗 根据回射声线路径和出射角方向，本文考虑的
糙海底近垂向大掠射角散射声场组成，实验海区海 海底散射路径分为 4 组，如图 6 所示：(a) 出射角向