Page 9 - 《应用声学》2021年第6期

第 40 卷 第 6 期 刘今等： 涌浪条件下的浅海表面声道脉冲声传播 805

的平均声速最高，因此，理论上，处于表面声道内的 隔不随深度变化而变化，为二次脉动信号。在每
水听器相较于其他深度的水听器应最先收到信号， 个距离上，观察上面几个水听器，二次脉动信号
而实验结果是下面的水听器先收到信号。经初步分 旁边均有一个相对较弱的信号，定义为第二个脉
析，这是因为实验期间接收阵发生倾斜，水听器的深 冲。其中距离为 16.23 km 时，二次脉动信号与第
度波动较大。 二个脉冲信号耦合在一起。对于接收距离分别为
尽管实验中未测量流向，无法确定阵倾斜的方 7.39 km、16.23 km、37.64 km 时，第二个脉冲与第
向，但可以根据垂直阵水听器及温深计的相对位置 一个脉冲的时延分别为 58 ms、64 ms、88 ms。可
和温深计测量的深度数据，估计出垂直阵在不同时 以发现第二个脉冲到达的时间随着传播距离增加
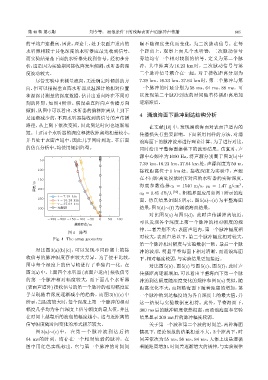
刻的阵形，如图 4 所示。假设垂直阵向声传播方向 逐渐滞后。
倾斜，从图中可以看出，水听器的偏移距离从上到下
4 涌浪海面下脉冲到达结构分析
是逐渐减少的，不同水听器接收到的信号的声传播
路径，从上到下依次变短，因此到达时间也逐渐缩 在文献 [10] 中，发现涌浪海面对表面声道内的
短。上面 4个水听器的深度和接收距离均相差较小， 传播损失有重要影响。下面采用同样的方法，对涌
并且处于表面声道中，因此几乎同时到达。在后面 浪海面下的脉冲波形进行理论计算。为了进行对比，
的仿真分析中，均使用倾斜阵型。 同时给出平整海面建模下的波形结果。仿真时，声

源中心频率为 1000 Hz，将声源分别置于图 2(b) 中
50
7.39 km、16.23 km、37.64 km 处，声源深度为 50 m，
100 接收距离位于 0 km 处。接收深度为实验中，声源
在不同距离处投放时所对应的水听器的实际深度。
150
ງए/m 200 海底参数选择 c b = 1540 m/s，ρ b = 1.47 g/cm ，
3
α b = 0.45 dB/λ [10] 。粗糙界面应用如图 1所示的海
r=7.39 km
250
r=16.23 km 面。仿真结果如图 5 所示，图 5(a)∼(c) 为平整海面
r=37.64 km
300 ௄Ϛப 结果，图5(d)∼(f)为涌浪海面结果。
对比图 5(a) 与图 5(d)，此时声传播距离较近，

-250 -200 -150 -100 -50 0 50 100
可以发现各个深度上第一个脉冲的相对幅度的规
Ϡረᡰሏ/m
律，二者差别不大：表面声道内，第一个脉冲幅度相
图 4 阵型
对较大，表面声道以下，第二个脉冲幅度相对较大，
Fig. 4 The array geometry
第一个脉冲相对幅度与实验数据一致。最后一个脉
对比图 3(a)(b)(c)，可以发现不同距离上的接 冲的波形，明显平整海面下相对清晰，而涌浪海面
收信号的脉冲幅度存在较大差异。为了便于比较， 下，相对幅度较弱，与实验结果更加接近。
图中每个深度上的信号均进行了单独归一化。在 对比图 5(b)、图 5(e) 与图 5(c)、图 5(f)，此时声
图 3(a) 中，上面四个水听器 (表面声道内) 接收信号 传播距离逐渐增加，可以看出平整海面下第一个脉
的第一个脉冲相对幅度较大，而下面几个水听器 冲的到达幅度随深度变化的规律和图 5(a) 类似，随
(表面声道外)接收信号的第一个脉冲的相对幅度近 距离变化不大；而粗糙海面下随着距离的增加，第
乎呈现随着深度逐渐减小的趋势。而图 3(b)(c) 中 一个脉冲的到达幅度均为各自深度上的最大值，并
所示，当距离较大时，每个深度上第一个脉冲的相对 这一结果与实验数据更相符。此外，平整海面下，
幅度几乎均为各自深度上信号幅度的最大值，并且 300 ms 后的脉冲幅度依然很强，而涌浪海面和实验
在时间上越靠后的波包的幅度越小。这与近距离的 结果显示300 ms后的脉冲幅度较弱。
信号幅度随时间变化的形式相差较大。 关于第一个波和第二个波的时间差，两种海面
图 3(a)∼(c) 中， 在 第 一 个 脉 冲 波 到 达 后 约 情况下，理论预报的结果相差不大。3 个距离下，时
64 ms 的时刻，均存在一个相对较弱的脉冲，在 间差依次为 55 ms、56 ms、84 ms，大体上也是遵循
图中用红色实线标出，它与第一个脉冲的时间间 着随距离增加，时间差逐渐增大的规律，与实验规律