Page 77 - 《应用声学》2022年第1期

第 41 卷 第 1 期 郭启超等： 采用子带二值加权累积的经验格林函数提取 73

数据验证了基于 SBWS 算法能够准确地提取 EGF 30.0
的时间结构，声速反演结果能正确反映水体温度的 29.5
日变化周期。 29.0
η٪උ/dB 28.5
EGF
3
0.5 Bellhop
1 28.0
ॆʷӑࣨϙ 0 27.5
27.0
200
-0.5 4 0 38 100 ߕࣜࣜࠕ/Hz 300 400
2
(a) EGFη٪උ
6
-1.0
2.2 2.3 2.4 2.5
௑ᫎ/s 5
(a) ଢԩᄊEGFˁBellhopေ᝷҂᣺௑ᫎࠫඋ 4
RMSE/(m·s -1 ) 3
1533.5
ࠄ฾ϙ
Ԧ໦ϙ
1533.0 2
ܦᤴ/(mSs -1 ) 1532.5 1 0 0 38 100 200 300 400

1532.0
ߕࣜࣜࠕ/Hz
1531.5 (b) ܦᤴԦ໦ឨࣀ
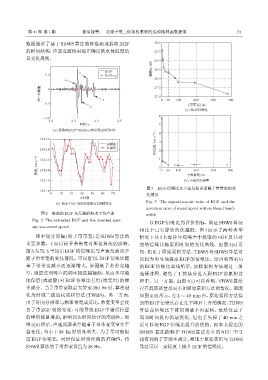
图 3 EGF 信噪比及声速反演误差随子带带宽的变
1531.0
0 12 24 36 48 60 72 化情况
࠵௑஝
Fig. 3 The signal-to-noise ratio of EGF and the
(b) ๒ඵࣱکܦᤴᄊԦ໦ϙˁࠄ฾ϙࠫඋ
inversion error of sound speed with subband band-
图 2 提取的 EGF 及反演的海水平均声速 width
Fig. 2 The extracted EGF and the inverted aver-
以 EGF 信噪比为评价指标，验证 SBWS 算法
age sea sound speed
相比于已有算法的优越性。图 4 展示了两种典型
频率划分间隔 (即子带带宽) 是 SBWS 算法的 情况下从 2 h 海洋环境噪声中提取的 EGF 及其对
重要参数，下面讨论子带带宽对所提算法的影响。 应的信噪比随累积时间的变化曲线。由图 4(a) 可
图 3 为 72 h 平均后 EGF 的信噪比与声速反演误差 知，相比于原始累积方法，TBWS 与 SBWS 算法可
随子带带宽的变化情况。可以看到，EGF 信噪比随 以较为明显地提高 EGF 的信噪比。原因如图 4(b)
着子带带宽减小而逐渐增大，原因是子带带宽越 的 EGF 信噪比曲线所示，加权累积方法通过二值
窄，则算法对噪声的频率挑选越精细，从而尽可能 选择过程，避免了干扰成分进入到 EGF 的累积过
地保留 (或滤除) 对 EGF 信噪比有用 (或无用) 的频 程中。另一方面，由图 4(c) 可以看到，TBWS 算法
率成分。当子带带宽取最大带宽 380 Hz 时，算法退 存在提取质量反而不如原始累积方法的情况。原因
化为时域二值加权累积算法 (TWBS)。另一方面， 如图 4(d) 所示，在 2 ∼ 40 min 内，原始累积方法得
由于时间分辨率与频率带宽成反比，带宽变窄会使 到的EGF信噪比存在先下降后上升的情况，TBWS
各子带 EGF 包络变宽，可能导致 EGF 中错误位置 算法在信噪比下降初期就不再累积，虽然保证了
的峰值能量增加，影响到达时间估计的准确性。如 局部时间段内的最优化，但也丢失掉了 40 min 之
图3(b) 所示，声速反演误差随着子带带宽变窄先平 后可以使 EGF 信噪比提升的快拍。而本文提出的
稳变化，当小于 38 Hz 时明显增大。为了尽可能提 SBWS 算法能够在 TBWS 算法舍弃的 NCF 中寻
高 EGF 信噪比，同时保证时间结构的准确性，将 找有利的子带频率成分，相比于原始累积与 TBWS
SBWS算法的子带带宽设置为38 Hz。 算法可以一定程度上提升EGF的信噪比。