Page 85 - 《应用声学》2022年第1期

第 41 卷 第 1 期 王凯等： 水声通信近似 L 0 范数约束的 BP 网络均衡器 81

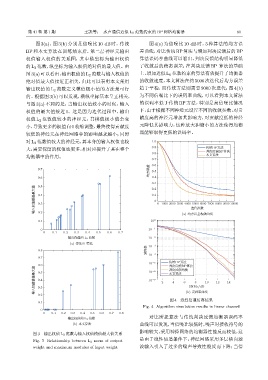
图 3(a)、图 3(b) 分别是信噪比 10 dB 时，传统 图 4(a) 为信噪比 10 dB 时，3 种算法的均方误
BP 和本文算法在训练结束后，第二层神经元输出 差曲线，对比传统 BP 算法与增加判决反馈后的 BP
权值输入权值的关系图，其中横坐标为输出权值 算法误码率曲线可以看出，判决反馈结构明显降低
的L 2 范数，纵坐标为输入权值绝对值的最大值。由 了收敛后的稳态误差；在判决反馈 BP 算法的基础
图 3(a)可以看出，输出权值的L 2 范数与输入权值的 上，增加近似 L 0 范数约束的算法有效提升了均衡器
绝对值最大值接近正相关，由此可以表明本文采用 的收敛速度，本文算法在约 5000次迭代后均方误差
输出权值的 L 2 范数定义模值极小值的方法是可行 趋于平稳，而传统方法则需要 9000 次迭代；图 4(b)
的。根据图 3(b) 可以发现，横纵坐标基本呈正相关， 为不同信噪比下的误码率曲线，可以看到本文算法
与图 3(a) 不同的是，当输出权值较小的时候，输入 的误码率低于传统 BP 方法，特别是高信噪比情况
权值的最大值接近 0。这是因为迭代过程中，输出 下，由于根据不同神经元设置不同的收敛参数，对贡
权值 L 2 范数值较小的神经元，其模值极小值会变 献度高的神经元增加其影响力，对贡献度低的神经
小，导致更多的权值向 0 收缩调整，最终使得贡献度 元降低其影响力，这种放大和缩小的方法使得均衡
较低的神经元在神经网络中的影响越来越小；同时 器能够取得更低的误码率。
对L 2 范数值较大的神经元，其本身的输入权值也较 1.0

大，需要保留的权值也更多，相对应提升了其在整个 0.9 ͜ፒBPካข
0.8 ѼхԦᯠBPካข
均衡器中的作用。 వ஡ካข
0.7
کவឨࣀ 0.5
0.7 0.6
0.6 0.4
0.3
0.5
ᣥКిϙവϙతܸϙ 0.4 0.1 0 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
0.2

0.3
ᤖ̽൓஝
0.2

0.1 10 0 (a) کவឨࣀஆகజጳ
0 10 -1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
ᣥѣిϙᄊ L 2 ᔵ஝ 10 -2
(a) ͜ፒBPካข 10 -3
ឨᆊဋ
0.8
0.7 10 -4
10 -5 ͜ፒBPካข
0.6 10 -6 ѼхԦᯠBPካข
ᣥКిϙവϙతܸϙ 0.4 10 -7 2 వ஡ካข 6 SNRb/dB 10 12 14
ѼхԦᯠکᛦ
0.5
4
8
0.3
0.2 (b) ឨᆊဋజጳ
图 4 线性信道仿真结果
0.1
Fig. 4 Algorithm simulation results in linear channel
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
ᣥѣిϙᄊ L 2 ᔵ஝ 对比所提算法与传统判决反馈均衡器误码率
(b) వ஡ካข 曲线可以发现，当信噪比较低时，噪声对接收符号的
影响较大，采用神经网络的均衡器性能反而较低，这
图 3 输出权值 L 2 范数与输入权值模值最大值关系
Fig. 3 Relationship between L 2 norm of output 是由于线性信道条件下，神经网络采用多层横向滤
weight and maximum modulus of input weight 波输入引入了过多的噪声导致性能反而下降；当信