Page 114 - 《应该声学》2022年第2期

282 2022 年 3 月

瑞利波频散曲线相对应的 β m ，对其取对数后再除 尽管匹配点 Q 对应的参数 β m 最大，但同时该模式
以 lg β m 中的最大值进行归一化处理，并以颜色的 产生的周期震荡二次谐波分量的幅值也较大，在一
变化在频散曲线上表示。图2 中相速度匹配点处的
1.0
β m 则反映实际匹配条件下对应基波模式能产生具 S2 S3 L S4 0.9
3000 S1
有线性累积效应二次谐波分量的强度。 0.8
根据 (9) 式可知，伴随基频瑞利波传播时所发 s7 Q 0.7
生的二次谐波声场可视为一系列二倍频瑞利波叠 c⊳(mSs -1 ) 2500 P s6 0.6 β m /m -2
0.5
2000
加而成，如点 P 对应频率处，竖直虚线 L 与二倍频 R s4 s5 0.4
1500 s1 s2 s3 0.3
瑞利波频散曲线存在一系列交点，这些交点对应的
0.2
二倍频瑞利波模式的叠加即表示伴随 S2 模式传播 1000
0.1
过程中所发生的二次谐波声场。根据理论部分的分 0
0 50 100 150 200
析可知，相速度匹配的模式均能激发出具有累积效 f/kHz
应的二次谐波，如图 2 所示该模型中 P 点和 Q 点对
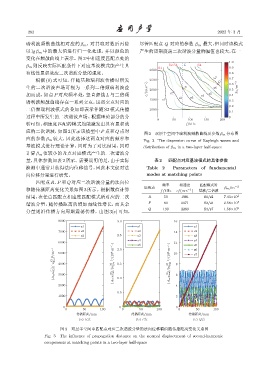
图 2 双层半空间中瑞利波频散曲线及参数 β m 分布图
应的参数 β m 较大，因此选择这两点对应的频率和 Fig. 2 The dispersion curve of Rayleigh waves and
基波模式进行理论计算，同时为了对比结果，同时 distribution of β m in a two-layer half-space
计算 β m 值较小的 R 点对应模式产生的二次谐波分
量，具体参数如表 2 所示。需要说明的是，由于实际 表 2 匹配点对应基波模式的具体参数
检测中通常只获得法向位移信号，因此本文仅对法 Table 2 Parameters of fundamental
向位移分量进行研究。 modes at matching points
匹配点 R、P 和 Q 对应二次谐波分量的法向位
匹配点 频率 相速度 匹配模式对 β m/m −2
移随传播距离变化关系如图 3 所示。根据数值计算 f/kHz c/(m·s −1 ) 基波/二倍波
结果，在任意匹配点相速度匹配模式所对应的二次 R 50 1901 S1/s2 7.43×10 3
谐波分量，随传播距离的增加而线性增长，而其余 P 80 2071 S2/s3 2.58×10 4
Q 190 2289 S4/s7 1.58×10 5
分量则沿传播方向周期震荡传播。由图 3(c) 可知，
8000 3.0 16
s1 s1 s1
7000 s2 s2 14 s2
s3 2.5 s3 s3
s4 s4
6000 2.0 s5 12 s5
A m u mz ⊳u Sz  2 /m -1 4000 (0) A m u mz ⊳u Sz  2 /(10 4 m -1 ) 1.5 (0) A m u mz ⊳u Sz  2 /(10 4 m -1 ) 8
s6
(0) 5000 10 s7
(1) 3000 (1) (1) 6

2000 1.0 4
0.5
1000 2

0 0 0
0 50 100 0 50 100 0 50 100
͜୧ᡰሏ/mm ͜୧ᡰሏ/mm ͜୧ᡰሏ/mm
(a) Rׄ (b) Pׄ (c) Qׄ
图 3 双层半空间中匹配点对应二次谐波分量的法向位移幅值随传播距离变化关系图
Fig. 3 The influence of propagation distance on the normal displacement of second-harmonic
components at matching points in a two-layer half-space