Page 77 - 《应该声学》2022年第2期

第 41 卷 第 2 期 宋华建等： 一种基于特征点提取的扬声器异常声检测方法 245

10 10 选空间金字塔数量i = 5，层数 n取3，构建空间金字
9 9
塔。进一步提取极值点，以中间层采样点为中心构
8 8
建 3×3×3 的采样空间如图 3 所示，将空间内的其余
7 7 26点与采样点比较，如果采样点为极大值或极小值，
ᮠဋ/kHz 6 5 4 ᮠဋ/kHz 6 5 4 则保留此采样点。

3 3
2 2
1 1
0 0.1 0.2 0.3 0.4 0.5 0 0.1 0.2 0.3 0.4 0.5
௑ᫎ/s ௑ᫎ/s Scale
(a) ៈฉࣜവ౜ (b) ᰴ൓ៈฉ۫വ౜
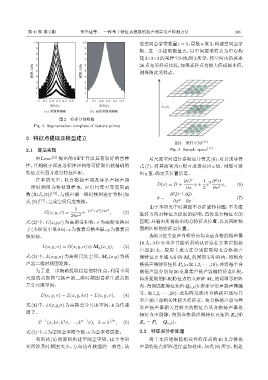
图 2 特征分割模板
Fig. 2 Segmentation template of feature points

2 特征点提取及模型建立
图 3 采样空间 [11]
2.1 算法实现 Fig. 3 Sample space [11]
由 Lowe [11] 提出的 SIFT 算法具有较好的鲁棒 对尺度空间进行泰勒展开得式(6)，对其求导得
性，且相较于深度卷积神经网络可提取出较精确的 式 (7)，将其值置为 0 则可求得对应 x 值，同理可得
特征点位置并进行特征匹配。 出y 值，确定其位置信息。
在本研究中，以合格扬声器及异常声扬声器 ∂D T 1 ∂ D
2
D(x) = D + x + x T x, (6)
二维时频图为待处理样本，应用尺度可变高斯函 ∂x 2 ∂x 2
2
数(如式 (2)) [12] ，与扬声器二维时频图进行卷积 (如 ∂ D −1 ∂D
ˆ x = − . (7)
式 (3)) [11] ，完成空间尺度变换。 ∂x 2 ∂x
由于本研究中时频图不存在旋转问题，不考虑
1 −(x +y )/2σ 2
2
2
G(x, y, σ) = e , (2) 旋转方向对特征点提取的影响，直接进行特征点的
2πσ 2
式 (2) 中，G(x,y,σ) 为高斯卷积核，σ 为高斯变换因 匹配，并输出所提取出的总特征点位置，以及两时频
子(本研究中取 0.6)，x 为像素点横坐标，y 为像素点 图相匹配的特征点位置。
纵坐标。 选取3 位专业声音检听员均认证合格的扬声器
10 支，3 位专业声音检听员均认证存在异常声的扬
L(x, y, σ) = G(x, y, σ) ⊗ M a (x, y), (3)
声器 20 支。应用上述方法分别提取每支合格扬声
式 (3) 中，L(x,y,σ) 为高斯尺度空间，M a (x,y) 为扬 器特征点并填入矩阵 M a 的同型零矩阵内，得到合
声器二维时频图矩阵。 格扬声器特征矩阵P a (a取1,2,· · · ,10)；并将每个合
为了进一步精确提取稳定的特征点，利用不同 格扬声器分别与 20 支异常声扬声器做特征点匹配，
尺度的高斯核与扬声器二维时频图卷积生成高斯 将所提取的匹配特征点填入矩阵M a 的同型零矩阵
差分尺度空间： 内，得到匹配特征矩阵 Q a,k (k 表示异常声扬声器编
号，取 1,2,· · · ,20)，此矩阵反映出合格扬声器与异
D(x, y, σ) = L(x, y, kσ) − L(x, y, σ), (4)
常声扬声器相关性较大特征点。将合格扬声器与异
式 (4) 中，D(x,y,σ) 为高斯差分尺度空间，k 为传递
常声扬声器相关性较大的特征点从合格扬声器总
因子。
特征点中剔除，得到合格扬声器特征点矩阵 Z a (即
2
2 i−1 (σ, kσ, k σ, · · ·, k n−1 σ), k = 2 1/n , (5) Z a = P a − Q a,k )。
式(5)中，i为空间金字塔个数，n为金字塔层数。 2.2 特征点分析处理
利用式 (5) 的原则构建空间金字塔，由于本研 将上文所述剔除相关性特征点的 10 支合格扬
究所涉及时频图大小、方向均有较强的一致性，故 声器特征点矩阵进行叠加处理，如式 (8) 所示，构建